Хипербола

За стилската фигура, погледајте ја Хипербола (лингвистика)

Хиперболи x²-y²=1 и y²-x²=1

Хипербола и нејзините 2 фокуса

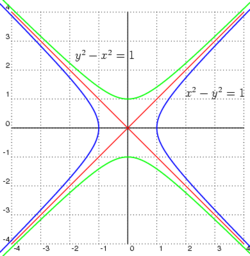
Хипербола (Предлошка:Lang-gr, претерување) – во математиката алгебарска крива од втор ред во рамнина, дадена со следната равенка: $\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$. Се состои од два симетрични дела, има жаришта и две асимптоти дадени со равенката $ay\pm bx=0$. Пресекот на асимптотите претставува центар на симетрија на хиперболата.

Хиперболата, заедно со параболата и елипсата, претставуваат три вида конусни пресеци. Конусните пресеци се добиваат во пресекот на рамнина со конусна површина (конусната површина се протега во двете насоки).

Равенки на хиперболата

Параметарските равенки на хиперболата се: $\{\begin{array}{c}x=a\sec \alpha \\ y=b\tan \alpha \end{array}$

Во Декартовиот координатен систем, хиперболата се опишува со равенката:

$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1.$

Особини

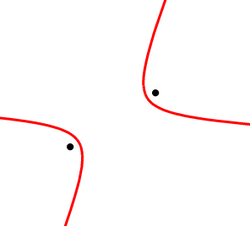
Постојат две важни особини на фокусите на хиперболата $F_1,F_2$:

1. За секоја точка на хиперболата Р, важи (d е растојанието): $\mid d(P,F_1)-d(P,F_2)\mid =2aa\in ℝ$
   Ова својство ја овозможува и следната дефиниција на хиперболата: Геометриско место точки во рамнина, за кои апсолутната вредност на разликата на растојанието од која било точка до две фиксни точки во истата рамнина (двата фокуса), е константна.
2. Тангентата на секоја точка на хиперболата Р претставува бисектриса $\mathrm{\angle }{F}_{1}P{F}_2$.

Поврзано

• Конусен пресек
• Елипса
• Парабола

Надворешни врски

• Информации за хиперболата