Лоренцов скалар

Во релативистичката теорија на физиката, Лоренцовиот скалар е израз, формиран од предмети од теоријата, која евалуира на скалар, непроменлив под каква било Лоренцова трансформација. Лоренцовиот скалар е генериран од на пр., скаларен производ на вектори, или од тензорите на теоријата. Додека компонентите на векторите и тензорите се вообичаено променети со Лоренцовите трансформации, Лоренцовиот скалар останува непроменет.

Лоренцовиот скалар не секогаш се смета дека е непроменлив скалар во математичка смисла, но добиената скаларна вредност е непроменлива под било која основна трансформација применета на векторскиот простор, на кој се заснова разгледуваната теорија. Едноставен Лоренцов скалар во Минковскиев простор е растојание во просторот ("должина" од нивната разлика) на два фиксни настани во просторот. Додека "позицијата" -4-вектори на настаните се менуваат помеѓу различните инерцијални рамки, нивното растојание во просторот останува непроменето под соодветната Лоренцова трансформација. Други примери за Лоренцов скалар се "должината" на 4-брзини (види подолу), или Ричиево искривување во точка во просторот од Општата теорија за релативноста,која е контракција на тензорот на Римановата кривина .

Едноставни скалари во специјалната релативност

Должината на положбениот вектор

Светски линии за две честички со различни брзини.

Во специјалната теорија за релативноста локацијата на честичка во 4-димензионалниот простор е дадена со

$x^{\mu }=(ct,𝐱)$

каде $𝐱=𝐯t$ е положбата во 3-димензионалниот простор на честичката, $𝐯$ е брзината во 3-димензионалниот простор и $c$ е брзината на светлината.

"Должината" на векторот е Лоренцов скалар и е даден со

$x_{\mu }{x}^{\mu }={\eta }_{\mu \nu }{x}^{\mu }{x}^{\nu }=(ct{)}^2-𝐱\cdot 𝐱\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}(c\tau {)}^2$

каде $\tau$ е вистинско време мерено со часовник во остатокот од рамката на честичката и Минковскиевата метрика е дадена со

${\eta }^{\mu \nu }={\eta }_{\mu \nu }=\left(\begin{array}{cccc}1& 0& 0& 0\\ 0& -1& 0& 0\\ 0& 0& -1& 0\\ 0& 0& 0& -1\end{array}\right)$.

Ова е метрика слична на времето.

Често е употребен алтернативниот потпис на Минковскиевата метрика во кој знаците на оние се обратни.

${\eta }^{\mu \nu }={\eta }_{\mu \nu }=\left(\begin{array}{cccc}-1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right)$.

Ова е метрика слична на просторот.

Во Минковскиевата метрика просторот како интервал $s$ е дефиниран како

$x_{\mu }{x}^{\mu }={\eta }_{\mu \nu }{x}^{\mu }{x}^{\nu }=𝐱\cdot 𝐱-(ct{)}^2\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}{s}^2$.

Ние ја користиме Минковскиевата метрика слична на просторот и во останатиот дел од поглавјето.

Должината на векторот на брзината

Вектори на брзина во просторот за честичка со две различни брзини. Во релативноста, забрзувањето е еквивалентно на ротацијата во просторот

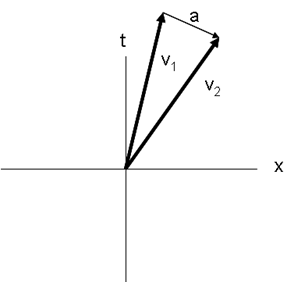
Брзината во просторот е дефинирана како

$v^{\mu }\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\frac{d{x}^{\mu }}{d\tau }=(c\frac{dt}{d\tau },\frac{dt}{d\tau }\frac{d𝐱}{dt})=(\gamma c,\gamma 𝐯)=\gamma (c,𝐯)$

каде

$\gamma \stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\frac{1}{\sqrt{1-\frac{𝐯\cdot 𝐯}{c^2}}}$.

Магнитудата на 4-брзина е Лоренцов скалар,

$v_{\mu }{v}^{\mu }=-c^2$.

Оттука, c е Лоренцов скалар.

Внатрешниот производ на забрзувањето и брзината

4-забрзување го дава

$a^{\mu }\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\frac{d{v}^{\mu }}{d\tau }$.

4-забрзување е секогаш нормално на 4-брзина

$0=\frac{1}{2}\frac{d}{d\tau }\left(v_{\mu }{v}^{\mu }\right)=\frac{d{v}_{\mu }}{d\tau }{v}^{\mu }=a_{\mu }{v}^{\mu }$.

Затоа, можеме да го сметаме забрзувањето во просторот како едноставна ротација на 4-брзина. Внатрешниот производ на забрзувањето и брзината е Лоренцов скалар и е нула. Оваа ротација е едноставно израз на конзервација на енергија:

$\frac{dE}{d\tau }=𝐅\cdot 𝐯$

каде $E$ е енергијата на честичката и $𝐅$ е 3-сила на честичката.

Енергија, останатата маса на честичката, 3-импулс и 3 брзина од 4-импулс

4-импулс на честичката е

$p^{\mu }=m{v}^{\mu }=(\gamma mc,\gamma m𝐯)=(\gamma mc,𝐩)=(\frac{E}{c},𝐩)$

каде $m$ е останатата маса на честичката, $𝐩$ е импулс во 3-простор, и

$E=\gamma m{c}^2$

е енергијата на честичката.

Мерење на енергијата на честичката

Да се разгледа втората честичка со 4-брзина $u$ и 3-брзина ${𝐮}_2$. Во остатокот од рамката на втората честичка внатрешниот производ $u$ with $p$ е пропорционален на енергијата на првата честичка

$p_{\mu }{u}^{\mu }=-E_1$

каде индексот 1 ја означува првата честичка.

Врската е точна во остатокот од рамката на втората честичка, таа е точна во секоја референтна рамка. $E_1$, енергијата на првата честичка во рамката на втората честичка е Лоренцов скалар. Затоа,

$E_1={\gamma }_1{\gamma }_2{m}_1{c}^2-{\gamma }_2{𝐩}_1\cdot {𝐮}_2$

во било која инерцијална референтна рамка, каде $E_1$ сè уште е енергијата на првата честичка во рамката на втората честичка.

Мерење на останатата маса на честичката

Во остатокот на рамката на честичката, внатрешниот производ на импулсот е

$p_{\mu }{p}^{\mu }=-(mc{)}^2$.

Затоа, останатата маса (m) е Лоренцов скалар. Врската останува точна независно од рамката во која се пресметува внатрешниот производ. Во многу случаи останатата маса е запишана како $m_0$ за да се избегне забуна со релативистичката маса, која е $\gamma m_0$

Мерење на 3-импулс на честичката

Забележи го следново

${(p_{\mu }{u}^{\mu }/c)}^2+p_{\mu }{p}^{\mu }=\frac{E_1^2}{c^2}-(mc{)}^2=({\gamma }_1^2-1)(mc{)}^2={\gamma }_1^2{𝐯}_1\cdot {𝐯}_1{m}^2={𝐩}_1\cdot {𝐩}_1$.

Квадратот на магнитудата на 3-импулсот на честичката, мерена во рамките на втората честичка, е Лоренцов скалар.

Мерење на 3-брзина на честичката

3-брзина, во рамката на втората честичка, може да се конструира од два Лоренцови скалари.

$v_1^2={𝐯}_1\cdot {𝐯}_1=\frac{{𝐩}_1\cdot {𝐩}_1{c}^4}{E_1^2}$.

Покомплицирани скалари

Скаларите, исто така, може да се конструираат од тензорите и векторите, од контракцијата на тензорите(како $F_{\mu \nu }{F}^{\mu \nu }$), или комбинации на контракции на тензори и вектори (како $g_{\mu \nu }{x}^{\mu }{x}^{\nu }$).

Наводи

• Предлошка:Наведена книга
• Предлошка:Наведена книга