Допуштени вредности (математичко образование)

Допуштени вредности

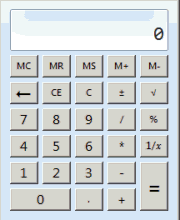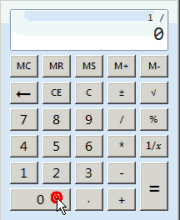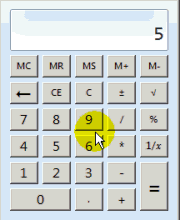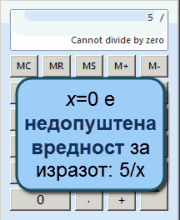
Дефиниција: За израз со променлива х, множеството на допуштени вредности D се сите реални броеви х за кои постои изразот. Основен пример: За изразот Предлошка:Дропка не се допуштува вредноста х=0. Ако во дигитрон типниме: 1 / 0 = ќе излезе дека е неможно, т.е. грешка (error). Сите други вредности можат да влегуваат во изразот наместо х. Значи, сите други вредности се допуштени вредности. Следува: Множеството на допуштени вредности на изразот Предлошка:Дропка се сите реални броеви освен 0. Пишиме: За   $\frac{1}{x}$,  $D=\{x|x\ne 0\}$ Означување и говор Множеството: {x|x ≠ 0} се чита „множеството на сите х такви што х не е еднакво на 0“. Еквивалентно имаме: $\mathrm{\Re }\setminus \{0\}$ кој се чита „сите реални броеви освен 0“. Еквивалентно имаме: x∈(-∞,0)(0,∞) кој се чита „х е реален број во интервалот од негативна бесконечност до нула унија интервалот од 0 до позитивна бесконечност“.

Ист е принципот и кај изрази со други променливи покрај или освен х.

Заклучок 1: Треба да се отстранат вредности на променливата (променливите) за кои именител би станал 0.

Други примери за допуштени вредности кај изрази со именители¹.

Израз	Услов за допуштени вредности	Допуштени вредности	Множеството на допуштени вредности
$\frac{2x^2-1}{x+1}$	$x+1\ne 0$	$x\ne -1$	$\mathrm{\Re }\setminus \{-1\}$ или $\{x|x\ne -1\}$
$\frac{x(7x^2-3y+2xz)}{-5y^{2}z}$	$-5y^{2}z\ne 0$	$y\ne 0$ и $z\ne 0$	$\{y,z|y\ne 0\wedge z\ne 0\}$
$\frac{7x^5-4x^3+2x^2-1}{x^2+3}$	$x^2+3\ne 0$	нема недопуштена вредност, т.е. x2+3 никогаш не е 0	$\mathrm{\Re }$ или $(-\mathrm{\infty },\mathrm{\infty })$
$\frac{-32x}{4x-3}$	$4x-3\ne 0$	$x\ne 0,75$	$\mathrm{\Re }\setminus \{0,75\}$
$\frac{a+b}{4}$	нема променлива во именителот	нема недопуштена вредност	$\mathrm{\Re }$
$\frac{3x^2-7xy+y^2}{y(1-x)}$	$y(1-x)\ne 0$	$y\ne 0$ и $x\ne 1$	$\{x,y|x\ne 1\wedge y\ne 0\}$
$\frac{a^2-b^2}{a-b}$	$a-b\ne 0$	$a\ne b$	$\{a,b|a\ne b\}$
$\frac{a^2-b^2}{4(a+b)}$	$4(a+b)\ne 0$	$a\ne -b$	$\{a,b|a\ne -b\}$
$\frac{3x+7}{2x^2-x-3}$	$2x^2-x-3\ne 0$	$x\ne 1,5$ и $x\ne -1$	$\{x|x\ne 1,5\wedge x\ne -1\}$ или (-∞,-1)(-1,1.5)(1.5,∞)
$\frac{3x}{x^2-2}+\frac{1}{2x}$	$x^2-2\ne 0$ и $2x\ne 0$	$x\ne \pm \sqrt{2}$ и $x\ne 0$	$(-\mathrm{\infty },-\sqrt{2})(-\sqrt{2},0)(0,\sqrt{2})(\sqrt{2},\mathrm{\infty })$

---

Основен пример 2: За изразот $\sqrt{x}$, не се допуштуваат негативни вредности, т.е. не се допуштуваат х < 0, односно се допуштуваат само ненегативни вредности (т.е. позитивни вредности и 0, х ≥ 0).

Значи: Множеството на допуштени вредности на изразот $\sqrt{x}$ се сите реални броеви x≥0.

Пишиме: За   $\sqrt{x}$,   $D=\{x|x\ge 0\}$

Заклучок 2: Треба да се отстранат вредности на променливата (променливите) за кои подкорениот израз би станал негативен.

Други примери за допуштени вредности кај изрази со квадратен корен.

Израз	Услов за допуштени вредности	Допуштени вредности	Множеството на допуштени вредности
$\sqrt{2x-6}$	$2x-6\ge 0$	$x\ge 3$	$x\in [3,\mathrm{\infty })$
$\sqrt{5(3-z)}$	$5(7-z)\ge 0$	$z\le 7$	$z\in (-\mathrm{\infty },7]$
$\frac{-2x^4-1}{\sqrt{x-4}}$	$x-4\ge 0$ и $x-4\ne 0$	$x>4$	$(4,\mathrm{\infty })$
$\frac{1-2x^4}{\sqrt{17,7}}$	нема променлива под корен, нуту во именител	нема недопуштена вредност	$\mathrm{\Re }$
$\sqrt{x^2+1}$	$x^2+1\ge 0$	нема недопуштена вредност, т.е. x2+1 е секогаш позитивен број	$\mathrm{\Re }$
$\sqrt{2x^2-x-3)}$	$2x^2-x-3\ge 0$	$x\le -1$ или $x\ge 1.5$	$x\in (-\mathrm{\infty };-1][1.5,\mathrm{\infty })$
$\frac{1}{\sqrt{3+2x-2x^2}}$	$3+x-2x^2>0$ или еквивалентно $2x^2-x-3<0$	$x>-1$ и $x<1.5$	$x\in (-1;1,5)$

Список основни изрази со ограничено множество на допуштени вредности

Израз	Множество на допуштени вредности	Коментар
$\frac{1}{x}$	{x| x≠0}	именител на дропка не смее да е 0
$\sqrt{x}$	{x| x≥0}	изразот под корен треба да е ненегативен
$\ln (x)$	{x| x>0}	(природен) логаритам постои само за позитивни броеви
$\log (x)$	{x| x>0}	логаритам (со основа 10) постои само за позитивни броеви
$\tan (x)$	{x| x ≠ Предлошка:Дропка, k=цел број}	tan(x)=Предлошка:Дропка. Значи tan(x) постои каде што cos(x)≠0, а cos(x)=0 за х=±Предлошка:Дропка, ±Предлошка:Дропка, ...
$\mathrm{asin}(x)$	{x| -1 ≤ x ≤ 1}	asin(x)=arcsin(x) e инверзна функција на sin(x)
$\mathrm{acos(x)}$	{x| -1 ≤ x ≤ 1}	acos(x)=arccos(x) e инверзна функција на cos(x)

Област на дефинираност на функција

Дефиниција: За функција y=f(x), множеството на сите допуштени вредности на аргументот х се вика областа на дефинираност D на функцијата f(x).

Рестрикција на функција

Дефиниција: Рестрикција на една функција y=f(x), е подмножеството на областа на дефинираност на функцијата на кое ние, како корисник на функцијата, ги ограничуваме можните влезни вредности (аргументи). Рестрикцијата може да биде било кое подмножество на D, но најчесто е поврзана со реалните можности на некоја конкретна задача.

¹Да се потсетите од логика или од теорија на множеста дека:

• Зборот „и“ = ∩ пресек на две множества = Λ конјункција на два изкази, а
• Зборот „или“ = ∪ пресек на две множества = V дисјункција на два изкази.

Литература

• http://en.wikipedia.org/wiki/Domain_of_a_function
• http://www.purplemath.com/modules/rtnldefs.htm

Други референции

• Функција (математичко образование)
• Област на дефинираност (математика)
• Рестрикција на функција (математика)
• http://www.wolframalpha.com/input/?i=domain+of+1%2Fx
• http://www.wolframalpha.com/input/?i=domain+of+sqrt(x)
• http://www.wolframalpha.com/input/?i=domain+of+ln%28x%29