Пи

Оваа статија е за бројот. За грчката буква видете пи (грчка буква). За други употреби видете пи (појаснување).

Кога пречникот на кругот е 1, неговата обиколка е Предлошка:Пи.

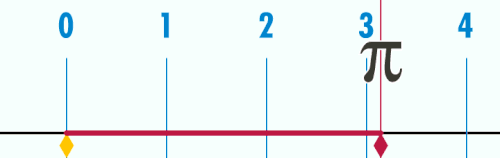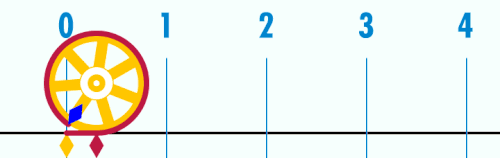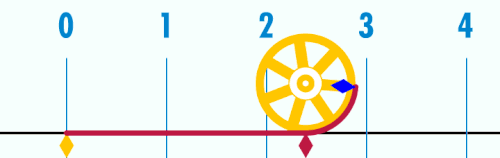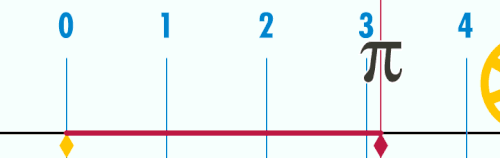
Пи (сим. Предлошка:Пи), Лудолфов број или Архимедова константа — ирационален реален број, кој го претставува односот на обиколката на една кружница со нејзиниот пречникот во Евклидовата геометрија. Бројот Предлошка:Пи има широка употреба во математиката, физиката и инженерството, но се употребува и во други науки. Бројот Предлошка:Пи исто така е познат и како Архимедова константа (што не е исто со Архимедов број) и како Лудолфов број (по германскиот математичар Лудолф ван Цојлен кој го пресметувал на многу децимали). Постојат различни начини за изразување на Архимедовата константа како дропка, еден од кои е дропката Предлошка:Дропка. Постојат брзи методи за добивање на бројот Предлошка:Пи со произволна точност. Неговата приближна вредност на 5 децимали изнесува 3,14159.

Буквата Предлошка:Пи

Името на [[Пи (буква)|грчката буква Предлошка:Пи]] е пи и овој запис се користи во типографски содржини каде што грчката буква не е достапна или каде што нејзината употреба би била проблематична. Константата се нарекува «Предлошка:Пи» бидејќи е првата буква од грчките зборови περιφέρεια (периферија) и περίμετρος (обиколка).

Предлошка:Пи е претставен со уникодниот знак U+03C0 („грчката мала буква пи“).

Дефиниција

Во Евклидовата рамнинска геометрија, Предлошка:Пи се дефинира како однос на обиколката на еден круг со неговиот пречник^[1], или како односот помеѓу плоштината на кругот со плоштината на квадрат чијашто страна е полупречник: $π = \frac{O}{d} = \frac{2 r π}{2 r} = π$
Константата Предлошка:Пи може да се дефинира на други начини кои го избегнуваат концептот на должина на лакот и плоштина, на пример како двапати по најмалиот позитивен x за кого sin(x) = 0.^[2] Формулите подолу ги илустрираат другите (еквивалентни) дефиниции.

Бројчена вредност

Бројчената вредност на Предлошка:Пи, скратена на 50 децимални места е:

3,14159 26535 89793 23846 26433 83279 50288 41971 69399 37510

Нема потреба за пресметување на Предлошка:Пи до милиони или милијарди цифри во практичната научна или инженерска работа. Вредност на Предлошка:Пи до 40 цифри би била повеќе од доволна да се пресмета обиколката на еден круг голем колку Млечниот Пат со грешка помала од големината на еден протон. Постојат неколку научни пресметки кои бараат извршување на посредни пресметки за значајно поголема прецизност на крајните резултати, но не е веројатно дека некому некогаш би му притребале повеќе од неколку стотици цифри од Предлошка:Пи за таква намера.

Сепак, точната вредност на Предлошка:Пи има бесконечен децимален дел: неговиот децимален дел не завршува никогаш и не се повторува, со оглед на тоа што Предлошка:Пи е ирационален број (и впрочем, трансцендентен број). Оваа бесконечна низа на цифри ги фасцинирала математичарите и лаиците, па така многу труд бил вложен во последните неколку векови со цел да се пресметаат повеќе цифри и да се истражат особините на бројот. И покрај сета аналитичка работа и суперкомпјутерски пресметки кои откриле над 1 билион цифри на Предлошка:Пи, никогаш не била пронајдена проста шема во цифрите. Цифрите на Предлошка:Пи се достапни на многу мрежни места, и постои софтвер за пресметување на Предлошка:Пи^[3] до милијардити цифри на кој било личен сметач. Видете [[историја на бројчените приближувања на Предлошка:Пи]].

Историја

Историски, за бројот Предлошка:Пи се знае од кога се знае и за самата математика.^[4] Некои автори, напредокот во тоа поле го делат на 3 периоди: антички, во кој бројот се пресметувал геометриски; класичен, во кој за неговата пресметка се користела напредната математика во Европа; и третиот дигитален период се однесува на компјутерското пресметување на бројот Предлошка:Пи.^[5]

Геометриски период

Тврдењето дека односот на лакот повлечен над права линија е околу 3 пати подолг од правата линија било познато уште во античко време. Тоа тврдење го знаеле староегипетските, вавилонските, индиските и старогрчките математичари. Најраните апроксимативни вредности на бројот Предлошка:Пи, датираат од околу 1900 п.н.е. и изнесуваат 25/8 (Вавилон) и 256/81 (Египет). И двете се со околу 1% отстапување од вистинската вредност.^[6] Во индискиот текст „Шатапатха Брамана“, вредноста на Предлошка:Пи е изразена како 339/108 ≈ 3,139. Во „Книга на кралевите“, во Танахот пишува дека Предлошка:Пи = 3. Таа вредност е воочливо понепрецизна од вредностите кои во тоа време биле познати (600 години п.н.е.).^[7]^[8]

Архимед (287-212 п.н.е.) бил првиот којшто точно ја пресметал вредноста на бројот Предлошка:Пи. Тој сфатил дека до точната вредност на плоштината на кругот може да се дојде со цртање на многуаголници во кругот, а од тоа и да се дојде до поточна вредност на Предлошка:Пи.

За да се стигне до поточна вредност потребно е да се нацрта многуаголник со што е можно поголем број на страни. Архимед нацртал 96-аголник и докажал дека 223/71 < Предлошка:Пи < 22/7.^[8]

Во следните векови, најголем напредок на тоа поле е постигнат во Индија и Кина. Околу 265 година, математичарот Лиу Хуи од кралството Веи, открил едноставен алгоритам за пресметување на вредноста на бројот Предлошка:Пи, до која било децимала. Тој тоа го пресметал на многуаголник со 3072 страни и го добил резултатот Предлошка:Пи=3,1416.

\begin{matrix} π ≊ A_{3072} & ≊ 768 \sqrt{2 - \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + 1}}}}}}}}} \\ ≊ 3, 14159 . \end{matrix}

Подоцна Лиу Хуи измислил [[Лиу Хуиев Предлошка:Пи алгоритам|алгоритам]], со кој се добивала вредноста Предлошка:Пи=3,1416, користејќи многуаголник од 96 страни, тврдејќи дека разликата на плоштината на последователните многуаголници дава геометриска прогресија со количник 4.

Околу 480 година, кинескиот математичар Цу Џунгџи ја дал приближната вредност Предлошка:Пи = 355/113, покажувајќи дека 3,1415926 < Предлошка:Пи < 3,1415927. Тоа го добил со помош на [[Лиу Хуиев Предлошка:Пи алгоритам|Лиу Хуиевиот Предлошка:Пи алгоритам]] за многуаголник со 12.288 страни. Тоа се покажало како најточно пресметан број во наредните 900 години.

Класичен период

До вториот милениум, бројот Предлошка:Пи бил со точност помала од 10 децимални места. Следниот голем напредок бил појавата на напредната математика и бесконечните низи. Тие низи теоретски даваат можност теоретски да се пресмета вредноста на Предлошка:Пи до која било децимала. Околу 1400 година, индискиот математичар Мадава од Сангамаграма ја открил првата позната низа од тој вид:

\frac{π}{4} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \dots

Не толку позната како Грегори-Лајбницова формула:

π = \sqrt{12} (1 - \frac{1}{3 \cdot 3} + \frac{1}{5 \cdot 3^{2}} - \frac{1}{7 \cdot 3^{3}} + \dots)

Мадхава успеал бројот да го пресмета со 11 децимали:

Предлошка:Пи = 3,14159265359

Рекордот е срушен во 1424 година од страна на персискиот астроном Јамшид ал Каши, кој бројот го пресметал со 16 децимали.

Првиот голем напредок во пресметувањето на бројот од времето на Архимед го направил германскиот математичар Лудолф ван Цојлен (1540-1610), кој со геометриски метод успеал да го пресмета бројот Предлошка:Пи со точност од 35 децимали. Тој бил толку среќен и горд со овој успех, така што добиената вредност била врежана на неговиот надгробен споменик.^[9]

Во истиот временски период, методите на напредната математика и одредувањето на бесконечните низи почнало да се развива во Европа. Прва позната формула била Виетовата формула,

\frac{2}{π} = \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{2 + \sqrt{2}}}{2} \cdot \frac{\sqrt{2 + \sqrt{2 + \sqrt{2}}}}{2} \cdot \dots

која ја открил Франсоа Виет во 1593. Друг познат резултат е Валисовиот производ,

\frac{π}{2} = \frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \dots

запишан од страна на Џон Валис во 1655. Исак Њутн измислил низа за пресметување на Предлошка:Пи со која можела да се пресметаат 15 децимали, иако подоцна самиот Њутн рекол: „Срам ми е да ви кажам колку фигури нацртав за оваа пресметка, немајќи некоја друга работа.“^[10]

Во 1706, Џон Мачин прв го пресметал бројот Предлошка:Пи со повеќе од 100 децимали, користејќи ја формулата

\frac{π}{4} = 4 \arctan \frac{1}{5} - \arctan \frac{1}{239}

при што ја користел формулата

\arctan x = x - \frac{x^{3}}{3} + \frac{x^{5}}{5} - \frac{x^{7}}{7} + \dots

Формулите од овој вид се познати како редни формули и биле употребувани, најчесто за подобрување на рекордот во точноста на пресметката на вредноста на бројот Предлошка:Пи, на што е можно поголем број на децимали.

Пресметката во дигиталниот период

Појавата на компјутерската технологија во 20 век довела до нов рекорд во пресметката на точноста на бројот Предлошка:Пи. Со помош на ENIAC, Џон фон Нојман пресметал број со 2037 цифри во 1949 година. За таа пресметка му биле потребни 70 часа. Со секоја наредна декада, бројот на децимални места при пресметките се зголемувал за неколку илјади, а во 1973 година, се дошло и до милионитата децимала.

Напредокот не бил само резултат на брзиот напредок во дигиталната технологија, туку и резултат на појавата на нови алгоритми. Голем напредок било откривањето на брзата Фуриеова трансформација во 1960 година, која овозможува аритметичко пресметување на екстремно големи броеви со многу голема брзина.

На почетокот на 20 век, индискиот математичар Сринивас Раманујан (1887—1920) открил многу нови формули за пресметување на вредноста на бројот Предлошка:Пи.^[11] Двете негови најпознати формули се:

\frac{1}{π} = \frac{2 \sqrt{2}}{9801} \sum_{k = 0}^{\infty} \frac{(4 k)! (1103 + 26390 k)}{(k!)^{4} 39 6^{4 k}}

и

\frac{426880 \sqrt{10005}}{π} = \sum_{k = 0}^{\infty} \frac{(6 k)! (13591409 + 545140134 k)}{(3 k)! (k!)^{3} (- 640320)^{3 k}}

кои даваат резултат со 14 децимали по пресметката.^[11] Браќата Чудновски работеле на оваа формула за неколку рекордни пресметки на крајот од 1980-тите, вклучувајќи ја и првата пресметка со над милијарда децимали (точно 1.011.196.691 децимали) во 1989 година. Ова формула останува и во пресметките на компјутерските програми, кои се користат за поставување на нови рекорди при пресметката на бројот Предлошка:Пи.

Формули

Геометрија

Пи се појавува во геометриските формули кои се однесуваат на геометриските слики и тела, кои содржат облик на круг или елипса. Во нив спаѓаат цилиндарот, конусот и топката.

Геометриски облик	Формула
Обиколка на круг со полупречник r односно пречник d	$O = π d = 2 π r$
Плоштина на круг со полупречник r	$P = π r^{2}$
Плоштина на елипса со полуоски a и b	$P = π a b$
Волумен на топка со полупречник r	$V = \frac{4}{3} π r^{3}$
Плоштина на топка со полупречник r	$P = 4 π r^{2}$
Волумен ан цилиндар со висина H и полупречник r	$V = π r^{2} H$
Плоштина на цилиндар со висина H и полупречник r	$P = 2 (π r^{2}) + (2 π r) H = 2 π r (r + H)$
Волумен на конус со висина H и полупречник r	$V = \frac{1}{3} π r^{2} H$
Плоштина на конус со висина H и полупречник r	$P = π r \sqrt{r^{2} + H^{2}} + π r^{2} = π r (r + \sqrt{r^{2} + H^{2}})$

Тригонометријата

Во тригонометријата, аголот од 180 степени изнесува Предлошка:Пи радијани.

Анализа

Во математичката анализа, бројот пи се изразува и користи на различни начини. Од обликот на бесконечни редови и производи до интеграли и специјални функции.

Франсоа Виет, 1593:

\frac{2}{π} = \frac{\sqrt{2}}{2} \frac{\sqrt{2 + \sqrt{2}}}{2} \frac{\sqrt{2 + \sqrt{2 + \sqrt{2}}}}{2} \dots

Лајбницова формула:

\frac{1}{1} - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} - \dots = \frac{π}{4}

Овој бесконечен ред, често се запишува во следниот облик:

\sum_{n = 0}^{\infty} (- 1)^{n} (\frac{1}{2 n + 1}) = \frac{π}{4}

Валисов производ:

\frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \dots = \frac{π}{2}

Интеграл на веројатноста, познат од математичката анализа:

\int_{- \infty}^{\infty} e^{- x^{2}} d x = \sqrt{π}

Базелски проблем, кој прв го решил Ојлер (видете исто така: Риманова зета-функција):

ζ (2) = \frac{1}{1^{2}} + \frac{1}{2^{2}} + \frac{1}{3^{2}} + \frac{1}{4^{2}} + \dots = \frac{π^{2}}{6}

ζ (4) = \frac{1}{1^{4}} + \frac{1}{2^{4}} + \frac{1}{3^{4}} + \frac{1}{4^{4}} + \dots = \frac{π^{4}}{90}

и воопшто

ζ (2 n)

е рационален производ

π^{2 n}

за секој природен број -{n}-.

Вредност на Гама-функцијата во точката 1/2:

Γ (\frac{1}{2}) = \sqrt{π}

Стирлингова апроксимативна формула:

n! \approx \sqrt{2 π n} {(\frac{n}{e})}^{n}

Ојлеров идентитет (којшто Ричард Филип Фајнман го нарекол „совршена математичка формула“):

e^{i π} + 1 = 0

Својства на Ојлеровата φ-функција:

\sum_{k = 0}^{n} ϕ (k) \sim 3 n^{2} / π^{2}

Плоштина на една четвртина од кругот:

\int_{0}^{1} \sqrt{1 - x^{2}} d x = \frac{π}{4}

Комплексна анализа

Специјален случај на Ојлеровата формула за $e^{i x}$ :

e^{i π} + 1 = 0

Основен случај на теоремата за остатоци:

\oint \frac{d z}{z} = 2 π i

Верижно разложување

Предлошка:Пи може да биде претставен како верижно разложување, како на пример:

\frac{4}{π} = 1 + \frac{1}{3 + \frac{4}{5 + \frac{9}{7 + \frac{16}{9 + \frac{25}{11 + \frac{36}{13 + . .}}}}}}

Теорија на броеви

Од теоријата на броеви се знае дека веројатноста два случајно избрани броеви да бидат заемно прости е 6/Предлошка:Пи², а истата веројатност е и при случајно избирање на еден број, тој да нема квадратен корен, кој е цел број. Во просек, бројот на даден природен број да се изрази како збир на два совршени квадрати е во просек Предлошка:Пи/4.

Динамични системи

Во теоријата на динамични системи (видете исто така: Ергодичка теорија), за скоро секој реален број -{x₀}- во интервалот [0, 1],

\lim_{n \to \infty} \frac{1}{n} \sum_{i = 1}^{n} \sqrt{x_{i}} = \frac{2}{π},

каде -{x_i} - интегрирани вредности на логистичкото пресликување -{r = 4}-.

Физика

Во физиката, бројот Предлошка:Пи се јавува во некои формули. На пример, бројот Предлошка:Пи е содржан во упростениот израз на формулата на Планковата константа $ℏ = \frac{h}{2 π}$ . Всушност упростената формула е основна, а присуството на факторот 1/2Предлошка:Пи во формулата со h може да се смета за условен од вообичаената дефиниција за Планковата константа:

Хајзенбергов принцип на неодреденост:

Δ x Δ p \geq \frac{h}{4 π}

Ајнштајново изедначување на полиња во општата теорија за релативноста:

R_{i k} - \frac{g_{i k} R}{2} + Λ g_{i k} = \frac{8 π G}{c^{4}} T_{i k}

Кулонов закон за електрична сила:

F = \frac{| q_{1} q_{2} |}{4 π ϵ_{0} r^{2}}

Магнетна пермеабилност на слободниот простор:

μ_{0} = 4 π \times 1 0^{- 7} H / m

Веројатност и статистика

Во веројатност и статистиката постојат голем број на распределби чии изрази го содржат бројот Предлошка:Пи. Меѓу нив спаѓаат и густината на распределба на веројатноста за нормална распределба со очекувана веројатност μ и стандардно отстапување σ:

f (x) = \frac{1}{σ \sqrt{2 π}} e^{- (x - μ)^{2} / (2 σ^{2})}

Густина на распределба на веројатноста (Кошиева распределба):

f (x) = \frac{1}{π (1 + x^{2})}

Треба да се забележи дека, како $\int_{- \infty}^{\infty} f (x) d x = 1$ за секоја функција на густината на распределба на веројатноста -{f(x)}-, со помош на горната формула може да се изведат други формули изразени преку Предлошка:Пи.

Интересна емпириска приближна вредност на бројот Предлошка:Пи се заснова на проблемот на Буфонова игла. Го разгледуваме експериментот, во кој игла со должина -{L}- се фрла на рамнина, на која се означени две паралелни прави со меѓусебно растојание -{S}- (каде што -{S}->-{L}-). Ако иглата, случајно се фрли голем број на пати, -{(n)}- од кои -{x}-, така што да пресекува една од правите, тогаш приближната вредност на бројот Предлошка:Пи може да ја добиеме со формулата:

π \approx \frac{2 n L}{x S}

Отворени прашања

Отвореното прашање за овој број е дали Предлошка:Пи е нормален број, дали постои децимала која би дала можност статистички да се предвидат останатите негови децимали. Ова мора да биде точно не само во декадниот систем. Моментно познавањата во оваа насока не се големи, па така не се знае ни кои цифри се јавуваат бесконечно, а кои не.

Во 2000 година, Бејли и Крендал покажаа дека со формулата Бејли-Борвајн-Плуфе и слични на неа формули може да се докаже нормалноста на бројот Предлошка:Пи и на други константи, во основа 2 може да се сведе на разумна претпоставка во теоријата на хаос.

Исто така не е познато дали броевите Предлошка:Пи и е се алгебарски независни, односно дали постои нетривијална полиномска релација меѓу овие два броја со рационални коефициенти.

Џон Харисон (1693—1776) создал музички систем организиран од Предлошка:Пи. Овој Луси тјунинг систем, (поради единството на математичките својства на бројот Предлошка:Пи) може да ги преслика сите музички интервали, хармонии и хармоники. Ова наложува дека користењето на Предлошка:Пи може да добие попрецизен модел како во музичките така и во другите вибрациони системи.

Природата на бројот Предлошка:Пи

Во хиперболичната геометрија, збирот на аглите на триаголник може да биде помал или поголем од Предлошка:Пи радијани, а односот на обиколка на кругот и неговиот пречник може да се разликува од Предлошка:Пи. Ова не ја менува неговата дефиниција, но влијае на многу формули каде Предлошка:Пи се појавува. Па, особено обликот на универзумот не влијае на Предлошка:Пи; Предлошка:Пи не е физичка константа, туку математичка константа, дефинирана независно од некои физички мерења. Причината зошто Предлошка:Пи се појавува така често во физиката е едноставно поради тоа што се содржи во многу физички модели. На пример, Кулоновиот закон:

F = \frac{1}{4 π ϵ_{0}} \frac{| q_{1} q_{2} |}{r^{2}}

.

Овде, $4 π r^{2}$ е плоштина на топка со полупречник r. Во оваа форма, ова е погоден начин за опишување на инверзната квадратна врска меѓу силата и растојанието r од изворот точка. Се разбира дека би било можно овој закон да се опише на друг начин, но сепак ова е најсоодветниот начин. Ако го користиме Планковото електризирање, Кулоновиот закон може да се опише како $F = \frac{q_{1} q_{2}}{r^{2}}$ за што се јавува потребата од Предлошка:Пи.

Ден на бројот пи

Предлошка:Главна

Податотека:ПИ-та од јаболки, Институт за Информатика-Скопје (март 2010).JPG

ПИ-та од јаболка на Институтот за информатика при УКИМ, Скопје

Денот на бројот пи и Денот на апроксимацијата на бројот пи се два празника кои се слават помеѓу математичарите ширум светот, а со кои се одбележува важноста на бројот Предлошка:Пи. Денот на бројот Предлошка:Пи во математичкиот свет се слави секој 14 март, зашто ако го напишете датумот во облик на м.дд тогаш се добива наједноставната апроксимација на бројот Предлошка:Пи: 3,14. Во некои земји каде датумот се запишува во формат дд.мм вообичаено како ден на бројот Предлошка:Пи се одбележува 22 јули, односно 22/7.

Еден од обичаите на денот е да се прави празнична пита која, со своето име, го симболизира бројот пи.

Пи како тема во уметноста и во популарната култура

„Бројот пи“ - песна на полската поетеса Вислава Шимборска.^[12]

Поврзано

Надворешни врски

Цифри

http://www.zenwerx.com/pi.php Предлошка:Семарх — околу 2 мегабајти во должина.
Пи до пет милиони места на Kick Books Предлошка:Семарх
http://www.gutenberg.net/etext/50 Предлошка:Семарх
Пребарајте ги првите 200 милиони цифри на Предлошка:Пи за произволни низи на броеви
Изворен код за пресметување на цифрите на Предлошка:Пи Предлошка:Семарх
Светска ранг листа за пи — Список на многу луѓе кои меморизирале голем број на цифри од Предлошка:Пи.

Општо

Радоста на пи од Дејвид Блатнер
Џеј Џеј О’Конор и Е. Ф. Робертсон: Историја на пи. Проект на Mac Tutor
Доказ дека Предлошка:Пи е ирационален
Многу формули за Предлошка:Пи на MathWorld
PlanetMath: Пи Предлошка:Семарх
Наоѓање на вредноста на Предлошка:Пи
Определување на Предлошка:Пи на cut-the-knot
Животот на пи од Џонатан Борвајн Предлошка:Семарх
BBC радио програма за Предлошка:Пи
Децимални делови на пи и поврзани врски на On-Line Encyclopedia of Integer Sequences
Статистички информации за пи Предлошка:Семарх засновани на 1,2 билиони цифри на пи

Наводи

Предлошка:Наводи

Предлошка:Избрана Предлошка:Ирационални броеви Предлошка:Нормативна контрола

↑ About Pi. Ask Dr. Math FAQ
↑ Рудин стр. 183
↑ Предлошка:Наведена мрежна страница
↑ Предлошка:Наведена книга
↑ Предлошка:Наведена мрежна страница
↑ http://mathforum.org/dr.math/faq/faq.pi.html
↑ Предлошка:Наведена мрежна страница
↑ ^8,0 ^8,1 Предлошка:Наведена мрежна страница
↑ Предлошка:Наведена книга
↑ The New York Times: Even Mathematicians Can Get Carried Away
↑ ^11,0 ^11,1 Предлошка:Наведена мрежна страница
↑ Vislava Šimborska, Izabrane pesme. Beograd: Treći trg, 2014, стр. 213-214.

[1] About Pi. Ask Dr. Math FAQ

[2] Рудин стр. 183

[3] Предлошка:Наведена мрежна страница

[4] Предлошка:Наведена книга

[5] Предлошка:Наведена мрежна страница

[6] ttp://mathforum.org/dr.math/faq/faq.pi.html

[7] Предлошка:Наведена мрежна страница

[ahop-8] 8,0 ^8,1 Предлошка:Наведена мрежна страница

[9] Предлошка:Наведена книга

[10] The New York Times: Even Mathematicians Can Get Carried Away

[rad-11] 11,0 ^11,1 Предлошка:Наведена мрежна страница

[12] Vislava Šimborska, Izabrane pesme. Beograd: Treći trg, 2014, стр. 213-214.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

Пи