Прамен (геометрија)

Некои прави од праменот со теме А

Во геометријата, прамен е фамилија од геометриски објекти со некое заедничко својство. На пример, прамен е множество од прави кои минуваат низ дадена точка во рамнината или множество од кружници кои минуваат низ две дадени точки во рамнината.

Иако дефиницијата за прамен е прилично нејасна, заедничка карактеристика е тоа што праменот е целосно определен од кои било два од неговите членови. Аналогно на тоа, множество од геометриски објекти кои се определени од кои било три негови члена се нарекува сноп. Така, множеството од сите прави кои минуваат низ една дадена точка во тридимензионален простор е сноп од прави, од кои секои две одредуваат прамен од прави. За да се нагласи дводимензионалната природа на таквиот прамен, тој понекогаш се нарекува и рамнински прамен од прави.

Секој геометриски објект може да се смета дека е во некој прамен. Вообичаени се прамените од прави, рамнини, кругови, конуси, сфери и од општи криви. Може да се користат дури и точки: прамен од точки е множество од сите точки на дадена права. Почест термин за ова множество е опсег на точки.

Прамен од прави

Нека Предлошка:Мпром и Предлошка:Мпром се две различни прави кои се сечат и лежат во дадена рамнина. За определеност, да претпоставиме дека Предлошка:Мпром е дадена со равенката Предлошка:Мат, а Предлошка:Мпром со равенката Предлошка:Мат. Тогаш, за секоја права што минува низ пресекот на правите Предлошка:Мпром и Предлошка:Мпром, постојат соодветни скалари Предлошка:Мпром и Предлошка:Мпром, такви што таа права е дадена со равенката

или кратко

Предлошка:Мат.

Ова множество од прави кои минуваат низ заедничка точка се нарекува прамен од прави. Заедничката точка на праменот од прави се нарекува теме или врв на праменот.

Во афина рамнина со рефлексивна варијанта на паралелизам, множество од сите меѓусебно паралелни прави формира класа на еквиваленција наречена прамен од паралелни прави. Оваа терминологија е конзистентна со горенаведената дефиниција бидејќи во единственото проективно продолжување на афината рамнина до проективна рамнина се додава една точка (бесконечна или идеална точка) на секоја права од праменот од паралелни прави, со што се добива прамен во горенаведената смисла во проективната рамнина.

Прамен од рамнини

Четири рамнини од осниот (аксијалниот) прамен на P1 P2

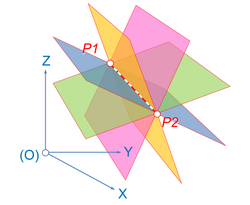
Прамен од рамнини е множество од рамнини во тридимензионалниот простор кои содржат дадена фиксна права. Правата која е заедничка за рамнините на даден прамен од рамнини се вика оска на праменот. Праменот понекогаш се нарекува осен или аксијален прамен, вентилатор од рамнини или сноп од рамнини. На пример, меридијаните на земјината топка се дефинирани со прамен од рамнини чија оска се совпаѓа со оската на ротација на Земјата.

Секои две рамнини кои се сечат во една фиксна права во тридимензионалниот простор ја одредуваат оската, па оттука и сите рамнини од снопот на кој тие му припаѓаат.

Четиридимензионалниот простор на кватерниони може да се гледа како аксијален прамен од комплексни рамнини кои делат иста реална права. Всушност, кватернионите содржат сфера од имагинарни единици, а пар антиподни точки на оваа сфера, заедно со реалната оска, генерираат комплексна рамнина. Унијата на сите овие комплексни рамнини ја сочинува 4-алгебрата на кватерниони.

Прамен од кружници

Аполониеви кружници, два ортогонални прамени од кружници

Кои било две кружници во рамнината имаат заедничка радикална оска - правата која се состои од сите точки кои имаат еднакви степени во однос на двете кружници. Прамен од кружници (или коаксијален систем) е множеството од сите кружници во рамнината од кои секои две имаат иста радикална оска. За да биде дефиницијата покомплетна, се вели дека секоја фамилија од концентрични кружници формираат прамен со бесконечната права како радикална оска.

Постојат пет типа на прамени на кружници. Двете фамилии од Аполониеви кружници на горната илустрација претставуваат два од нив. Секој тип се одредува со две кружници наречени генератори на праменот. Кога прамените се опишуваат алгебарски, можно е равенките да примаат имагинарни решенија. Различните видови се:

• Елиптичен прамен (семејството од црвени кружници на цртежот) се дефинира со два генератора кои се сечат во точно две точки. Секоја кружница од елиптичен прамен поминува низ истите две точки. Во елиптичен прамен нема никакви имагинарни кружници.
• Хиперболичен прамен (фамилијата од сини кружници на цртежот) се дефинира со два генератора кои не се сечат еден со друг во ниту една точка. Секој хиперболичен прамен вклучува реални кружници, имагинарни кружници и две дегенерирани кружници - точки наречени точки на Понселе на праменот. Секоја точка од рамнината припаѓа на точно една кружница од праменот.
• Параболичен прамен (како граничен случај) се дефинира кога двете генерирачки кружници се допираат во една точка. Се состои од семејство од реални кружници, сите тангентни една на друга во една заедничка точка. На праменот му припаѓа и дегенерираната кружница со радиус нула во таа точка.
• Семејство од концентрични кружници (може да се смета за посебен случај на хиперболичен прамен за кој едната точка на Понселе е заедничкиот центар, а другата точка на Понселе е бесконечнaта точка).
• Семејството од прави кои минуваат низ заедничка точка; овие прави треба да се толкуваат како кружници кои минуваат низ бесконечната точка (може да се смета за посебен случај на елипсовиден прамен).

Својства

Кружница која е ортогонална на две фиксни кружници е ортогонална на секоја кружница од праменот што тие го одредуваат.

Кружниците кои се ортогонални на две фиксни кружници формираат прамен од кружници (ортогонален прамен на праменот кој е определен со двете кружници).

Две кружници определуваат два прамена, единствениот прамен кој ги содржи нив и праменот од кружници кои се ортогонални на нив. Радикалната оска на еден од прамените се состои од центрите на кружниците на другиот прамен. Ако едниот прамен е од елиптичен тип, другиот е од хиперболичен тип и обратно. Ако едниот прамен е од параболичен тип, неговиот ортогонален прамен е, исто така, параболичен.

Радикалната оска на кој било прамен од кружници, толкувана како кружница со бесконечен радиус, му припаѓа на праменот. Кои било три кружници припаѓаат на заеднички прамен секогаш кога сите три пара имаат иста радикална оска и нивните центри се колинеарни.

Проективен простор од кружници

Постои природна кореспонденција помеѓу кружниците во рамнината и точките во тродимензионалниот проективен простор; права во овој простор одговара на еднодимензионално непрекинато семејство од кружници, па оттука, прамен од точки во овој простор е прамен од кружници во рамнината.

Поконкретно, равенката на кружница со радиус Предлошка:Мат и центар во точката (Предлошка:Мат) гласи

$(x-p{)}^2+(y-q{)}^2=r^2,$

а може да се запише и како

$\alpha (x^2+y^2)-2\beta x-2\gamma y+\delta =0,$

каде Предлошка:Мат. Во оваа форма, множењето на четворката (Предлошка:Мат) со скалар дава различна четворка која претставува иста кружница; така, ваквите четворки може да се сметаат како хомогени координати за просторот од кружници. Секоја права може да се претстави со равенка од овој тип во која Предлошка:Мат и треба да се смета дека е дегенерирана форма на кружница. Кога Предлошка:Мат, можеме да решиме за Предлошка:Мат, и $r=\sqrt{p^2+q^2-\delta /\alpha }$; последната формула може да даде Предлошка:Мат (тогаш кружницата дегенерира до точка) или Предлошка:Мат еднаков на имагинарен број (во тој случај се вели дека четворката (Предлошка:Мат) претставува имагинарна кружница).

Множеството од афини комбинации од двете кружници ( Предлошка:Мат ), ( Предлошка:Мат ), односно множеството од кружници претставени со четворката

$z({\alpha }_1,{\beta }_1,{\gamma }_1,{\delta }_1)+(1-z)({\alpha }_2,{\beta }_2,{\gamma }_2,{\delta }_2)$

за некоја вредност на параметарот Предлошка:Мат, формира прамен; двете кружници се викаат генератори на праменот.

Кардиоидата како обвивка (енвелопа) на прамен од кружници

Кардиоидата како обвивка (енвелопа) на прамен од кружници

Друг тип на прамен од кружници може да се добие на следниов начин. Замислете дадена кружница (наречена генераторна кружница) и една точка Предлошка:Мпром на неа. Множеството од сите кружници кои минуваат низ точката Предлошка:Мпром и имаат центри на генераторната кружница формираат прамен од кружници. Обвивката (енвелопата) на овој прамен е кардиоида.

Прамен од сфери

Сферата е еднозначно определена со четири точки кои не се компланарни, а меѓу кои секои три не се колинеарни. Поопшто, сферата е целосно одредена со четири независни услова како на пример: да минува низ точка, да биде тангентна на рамнина итн.

Следствено, сферата е еднозначно одредена со (т.е. поминува низ) кружница и точка која не е во рамнината на таа кружница.

Со испитување на заедничките решенија на равенките на две сфери, може да се види дека тие две сфери се сечат во кружница. Рамнината која ја содржи пресечната кружница на двете сфери се нарекува радикална рамнина на тие сфери. Иако радикалната рамнина е реална рамнина, кружницата може да биде имагинарна (кога сферите немаат реална заедничка точка) или да се состои од една точка (кога сферите се допираат во таа точка).

Ако Предлошка:Мат и Предлошка:Мат се равенките на две различни сфери тогаш

$\lambda f(x,y,z)+\mu g(x,y,z)=0$

е во исто време равенка на сфера за произволни вредности на параметрите $\lambda$ и $\mu$. Множеството од сите сфери што ја задоволуваат оваа равенка се нарекува прамен од сфери определени од првобитните две сфери. Во оваа дефиниција е дозволено сферата да биде рамнина (бесконечен радиус, центар во бесконечна точка). Ако двете првобитни сфери се рамнини, тогаш сите сфери од праменот се рамнини; инаку има само по една рамнина (радикалната рамнина) во прамен.

Ако праменот од сфери не се состои само од рамнини, тогаш постојат три вида прамени определени од две сфери:

• ако сферите се сечат во реална кружница C, тогаш праменот се состои од сите сфери кои ја содржат C, вклучувајќи ја и радикалната рамнина. Центрите на сите обични сфери во праменот лежат на права линија која минува низ центарот на C и е нормална на радикалната рамнина;
• ако сферите се сечат во имагинарна кружница, тогаш сите сфери на праменот, исто така минуваат низ оваа имагинарна кружница, но како обични сфери тие се разединети (немаат реални заеднички точки). Центрите на сферите од праменот лежат на права (централна права) која е нормална на радикалната рамнина, која е реална рамнина во праменот што ја содржи имагинарната кружница;
• ако сферите се допираат во точка A, сите сфери од праменот се допираат во A, а радикалната рамнина е заедничката тангентна рамнина на сите овие сфери. Централната права е нормална на радикалната рамнина на A.

Сите тангентни растојанија од фиксна точка на радикалната рамнина кон сферите на праменот имаат иста должина.

Радикалната рамнина е геометриско место од точки (локус) на центрите на сите сфери кои се ортогонални на сите сфери од праменот. Покрај тоа, сфера која е ортогонална на кои било две сфери од даден прамен од сфери е ортогонална на сите сфери од праменот и нејзиниот центар лежи во радикалната рамнина на праменот.

Прамен од коники

Коника која не е дегенерирана е целосно определена со пет точки во општа положба (т.е. меѓу точките нема три кои се колинеарни) во рамнина и системот на коники кои минуваат низ фиксна група од четири точки (кои повторно се компланарни и меѓу кои нема три колинеарни) се нарекува прамен од коники. Четирите заеднички точки се нарекуваат основни точки на праменот од коники. Низ која било точка различна од основните точки, поминува точно една коника од праменот. Овој концепт е обопштувње на поимот прамен од кружници.

Во проективна рамнина дефинирана преку алгебарски затворено поле, кои било две коники се сечат во четири точки (броени според кратноста) и така го определуваат праменот од коники за овие четири точки. Понатаму, четирите базни точки одредуваат три пара од прави (дегенерирани коники низ основните точки, секоја права од парот содржи точно две базни точки) и така секој прамен од коники ќе содржи најмногу три дегенерирани коники.

Прамен од коники може да се претстави алгебарски на следниов начин. Нека Предлошка:Мат и Предлошка:Мат се две различни коники во проективна рамнина дефинирана преку алгебарски затворено поле Предлошка:Мат. За секој пар Предлошка:Мат од елементи на Предлошка:Мат, такви што двата не се нула, изразот:

$\lambda C_1+\mu C_2$

претставува коника од праменот определен со Предлошка:Мат и Предлошка:Мат . Оваа симболична претстава може да се конкретизира со мала злоупотреба на ознаката (користејќи ја истата нотација за означување на објектот како и за равенката која го дефинира објектот.) Размислувајќи за Предлошка:Мат, да речеме, како за тернарна квадратна форма, тогаш Предлошка:Мат е равенката на „кониката Предлошка:Мат“. Друга конкретна реализација може да се добие со ако Предлошка:Мат се набљудува како симетрична 3×3 матрица која ја претставува. Ако Предлошка:Мат и Предлошка:Мат имаат такви конкретни реализации, тогаш таква реализација ќе има и секој член од горенаведениот прамен. Бидејќи во овој начин се користат хомогени координати во проективна рамнина, две конкретни репрезентации (равенки или матрици) даваат иста коника ако се разликуваат за ненулта мултипликативна константа.

Прамен од рамнински криви

Поопшто, прамен е посебен случај на линеарен систем на делители во кој параметарскиот простор е проективна линија. На пример, типичните прамени од криви во проективната рамнина може да се запишат како

$\lambda C+\mu C^{\prime }=0$

каде што со $C=0$ и $C^{\prime }=0$ се дадени две рамнински криви.

Историја

Дезарг е заслужен за измислувањето на терминот „прамен од прави“ (ordonnance de lignes).

Еден од рaните автори на модерната проективна геометрија Г. Б. Халстед ги вовел термините копунктални и рамни прамени за да го дефинира поимот агол: „Правите кои минуваат низ иста точка се копунктални“. Исто така „Множеството од сите компланарни, копунктални прави се нарекува рамнински прамен“ и „Дел од рамнински прамен ограничен со две од правите како страни, се нарекува агол“.

Поврзано

• Подесување на прамен
• Прамен на Лефшец
• Прамен од матрици
• Прамен од полуправи (зраци)
• Фибрација
• Геометриско место од точки (локус)

Наводи

• Предлошка:Наведување
• Предлошка:Наведување
• Предлошка:Наведување
• Предлошка:Наведување
• Предлошка:Наведување
• Предлошка:Наведување
• Предлошка:Наведување
• Предлошка:Наведување
• Предлошка:Наведување.
• Предлошка:Наведување
• Предлошка:Наведување

Надворешни врски

• Предлошка:MathWorld