Логаритам

Криви на логаритамски функции со најчесто користените основи

Логаритам — број што го покажува степенот на кој треба да се дигне основниот број за да се добие бараниот број. Логаритмот е обратна операција на степенувањето, исто како што делењето е обратна операција на множењето и обратно. Тоа значи дека логаритам од некој број е степенот на којшто друг број треба да се степенува за да истиот се добие. Во наједноставен случај логаритмот ги брои повторените множења на ист множител, на пример, бидејќи Предлошка:Math, „логаритмот со основа Предлошка:Math“ од Предлошка:Math е Предлошка:Math. Поопшто, степенувањето овозможува кој било реален број да се степенува на кој било степен, притоа дава позитивен резултат, така што може да се пресмета логаритам за кои било два позитивни реални броеви Предлошка:Math и Предлошка:Math каде Предлошка:Math е различен од Предлошка:Math. Логаритам од Предлошка:Math со „основа“ Предлошка:Math, обележан како Предлошка:Math (или Предлошка:Math за да нема забуни), е единствениот реален број Предлошка:Math така што Предлошка:Math. На пример, Предлошка:Math, со оглед дека Предлошка:Math.

Логаритмот со основа Предлошка:Math (што значи Предлошка:Math) се нарекува десетичен логаритам и има бројни примени во науката и инженерството. Природниот логаритам за основа го има [[е (математичка константа)|бројот Предлошка:Math]] (Предлошка:Math), и истиот нашироко се користи во математиката и физиката заради неговиот поедноставен извод. Основата на двоичниот логаритам е Предлошка:Math (така што Предлошка:Math) и се користи во информатиката.

Логаритмите биле воведени од Џон Непер на почетокот на XVII век како средство за поедноставување на пресметките. Брзо биле прифатени од морепловците, научниците, инженерите и други за поедноставно пресметување со користење на логаритмари и логаритамски таблици. Заморните чекори на множење на повеќецифрени броеви може да се заменат со податоци од табела и поедноставното собирање заради тоа што логаритам од производ е збир од логаритмите од множениците:

${\log }_b(xy)={\log }_{b}x+{\log }_{b}y,$

под услов Предлошка:Math, Предлошка:Math и Предлошка:Math да се позитивни и Предлошка:Math.

Денешниот поим за логаритам доаѓа од Леонард Ојлер, кој го поврзал логаритмот со експоненцијалната функција во XVIII век.

Логаритамските скали го смалуваат широкиот распон на количини на мали опсези. На пример, децибелот (dB) се користи како мерна единица за да изрази логаритамски однос, најчесто за моќ и амплитуда на сигнали (на пример звучен притисок). Во хемијата, pH е логаритамска мерка на киселоста на воден раствор. Логаритмите се вообичаени во научните формули, во мерењата на комплексноста на алгоритмите и геометриски објекти наречени фрактали. Помагаат да се опишат честотните соодноси на музичките интервали, се јавуваат во формулите за броење на примарни броеви, а можат да помогнат и во форензичкото сметководство.

Мотивација и дефиниција

Идејата на логаритмот е да биде обратна операција на операцијата степенување, која претставува дигање на некој број на степен. На пример, трет степен (или куб) од 2 е 8, бидејќи 8 е производ од три множеници по 2:

$2^3=2\times 2\times 2=8$

Следи дека логаритам од 8 со основа 2 е 3, па Предлошка:Math.

Степенување

Трет степен од некој број Предлошка:Mvar е производ на три множеници еднакви на Предлошка:Mvar. Поопшто, дигање на бројот Предлошка:Mvar на Предлошка:Nowrap степен, каде Предлошка:Mvar е природен број, се добива со множење Предлошка:Mvar множеници еднакви на Предлошка:Mvar. Предлошка:Nowrap степен од Предлошка:Mvar се пишува како Предлошка:Math, така што

$b^n=\underset{n\text{ factors}}{\underbrace{b\times b\times \cdots \times b}}$

Степенувањето може да се прошири на Предлошка:Math, каде Предлошка:Mvar е позитивен број, а „степенот“ Предлошка:Mvar е кој било реален број. На пример, Предлошка:Math е реципрочна на Предлошка:Mvar, што е, Предлошка:Math. (За повеќе поединости видете степенување или )

Дефиниција

Логаритам од позитивен реален број x со основа b, каде што b е позитивен реален број различен од 1,Предлошка:Refn е степенот на кој b треба да се крене за да се добие x. Со други зборови, логаритам од x со основа b е решението y на равенката

$b^y=x$

Логаритмот се бележи "Предлошка:Math" (се изговара „логаритам од x со основа b"), така што горниот дефинициски идентитет станува:

$b^{{\log }_{b}x}=x$

Во равенката Предлошка:Math, вредноста y е одговор на прашањето „На кој степен треба да се дигне b за да се добие x?“.

Примери

• Предлошка:Math, бидејќи Предлошка:Math.
• Логаритмите можат да бидат и негативни: ${\log }_2\frac{1}{2}=-1$ бидејќи $2^{-1}=\frac{1}{2^1}=\frac{1}{2}.$
• Предлошка:Math е приближно 2,176, што е меѓу 2 и 3, исто како што 150 лежи меѓу Предлошка:Math и Предлошка:Math
• За која било основа b, Предлошка:Math и Предлошка:Math, бидејќи Предлошка:Math и Предлошка:Math, соодветно.

Логаритамски идентитети

Предлошка:Главна Повеќе битни формули, наречени и логаритамски идентитети или логаритамски закони, ги даваат меѓусебните врски на логаритмите.

Производ, количник, степен, и корен

Логаритам од производ е сума од логаритмите од броевите кои се множат; логаритам од количник од два броја е разлика од логаритмите на деленикот и делителот. Логаритам од Предлошка:Nowrap степен на број е p пати од логаритмот од самиот тој број; логаритам од Предлошка:Nowrap корен е логаритам од бројот поделен со p. Во следната табела е даден список на идентитети со примери. Секој од идентитетите може да биде изведен со замена на дефинициите за логаритам $x=b^{{\log }_{b}x}$ или $y=b^{{\log }_{b}y}$ на левата страна од идентитетот.

	Формула	Пример
Производ	${\log }_b(xy)={\log }_{b}x+{\log }_{b}y$	${\log }_{3}243={\log }_3(9\cdot 27)={\log }_{3}9+{\log }_{3}27=2+3=5$
Количник	${\log }_b\frac{x}{y}={\log }_{b}x-{\log }_{b}y$	${\log }_{2}16={\log }_2\frac{64}{4}={\log }_{2}64-{\log }_{2}4=6-2=4$
Степен	${\log }_b\left(x^p\right)=p{\log }_{b}x$	${\log }_{2}64={\log }_2\left(2^6\right)=6{\log }_{2}2=6$
Корен	${\log }_b\sqrt[p]{x}=\frac{{\log }_{b}x}{p}$	${\log }_{10}\sqrt{1000}=\frac{1}{2}{\log }_{10}1000=\frac{3}{2}=1,5$

Промена на основата

Логаритмот Предлошка:Math може да биде пресметан од логаритмите на x и b со која било произволна основа k користејќи ја следната формула:

${\log }_{b}x=\frac{{\log }_{k}x}{{\log }_{k}b}.$

Предлошка:Collapse top Почнувајќи од дефиницискиот идентитет

$x=b^{{\log }_{b}x}$

Можеме да ги логаритмираме со Предлошка:Math двете страни од равенката и ќе добиеме

${\log }_{k}x={\log }_k(b^{{\log }_{b}x})={\log }_{b}x\cdot {\log }_{k}b$.

Решавајќи по ${\log }_{b}x$ добиваме:

${\log }_{b}x=\frac{{\log }_{k}x}{{\log }_{k}b}$,

Што го покажува факторот на претворање од дадените ${\log }_k$-вредности до нивните соодветни ${\log }_b$-вредности кои треба да бидат $({\log }_{k}b{)}^{-1}.$ Предлошка:Collapse bottom

Типичен научно сметало пресметува логаритми со основи 10 и e. Логаритми со која било основа b може да се определат користејќи кој било од овие два логаритма според претходната формула:

${\log }_{b}x=\frac{{\log }_{10}x}{{\log }_{10}b}=\frac{{\log }_{e}x}{{\log }_{e}b}.$

Со дадениот број x и неговиот логаритам Предлошка:Math со непозната основа b, основата е дадена со:

$b=x^{\frac{1}{{\log }_{b}x}},$ што може да се види од дефинициската равенка $x=b^{{\log }_{b}x}$ на степен $\frac{1}{{\log }_{b}x}.$

Посебни основи

Графици на логаритми со основи 0,5, 2 и e

Графиконот на логаритам со основа 2 ја минува x оската (хоризонталната оска) во 1 и минува низ точките со координати Предлошка:Nowrap, Предлошка:Nowrap, и Предлошка:Nowrap. На пример, Предлошка:Math, бидејќи Предлошка:Math. Кривата се приближува произволно блиску до y оската, но не ја допира или сече.

Меѓу сите избори за основа, три се особено чести. Тоа се Предлошка:Math, Предлошка:Math (ирационална математичка константа ≈ 2,71828), и Предлошка:Math (двоичен логаритам). Во математичката анализа, логаритмот со основа e се користи нашироко заради неговите посебни аналитички својства објаснети подолу. Од друга страна, логаритмите со основа Предлошка:Nowrap се лесни за користење при рачни пресметки во децималниот броен систем:

${\log }_{10}(10x)={\log }_{10}10+{\log }_{10}x=1+{\log }_{10}x.$

Така, Предлошка:Math се однесува на бројот на декадни цифри на позитивен цел број x: бројот на цифри е најмалиот цел број строго поголем од log₁₀x. На пример, Предлошка:Math е приближно еднаков на 3,15. Следниот цел број е 4, кој го дава бројот на цифри на 1430. И двата, природниот логаритам и двоичниот логаритам се користат во теоријата на информации, а како основни единици за информација ги користат натовите и битовите, соодветно. Двоичните логаритми исто така се користат во информатиката, каде двоичниот броен систем е сеприсутен, во музичката теорија каде што е сеприсутен во односот меѓу две октави, и во фотографијата за мерење на вредноста на експозиција.

Во следната табела се дадени најчестите обележувања за логаритмите со овие основи и полиња на нивната примена. Во многу дисциплини се пишува Предлошка:Math наместо Предлошка:Math, каде што основата може да се одреди од контекстот. Се користи и обележувањето Предлошка:Math. Колоната „ИСО обележување“ ги дава обележувањата препорачани од Меѓународната организација за стандардизација. Бидејќи обележувањето Предлошка:Math се користи за сите три основи (или кога основата е неопределена или нематеријална), основата треба да произлезе врз основа на контекстот или дисциплината. Во информатиката и математиката, вообичаено log се однесува на Предлошка:Math и Предлошка:Math, соодветно. Во други контексти log често значи Предлошка:Math.

Основа b	Име на logbx	ISO обележување	Други обележувања	се користи во
2	двоичен логаритам	Предлошка:Math	Предлошка:Math, Предлошка:Math, Предлошка:Math, Предлошка:Math	информатика, теорија на информациите, теорија на музиката, фотографија
e	природен логаритам	Предлошка:MathПредлошка:Refn	Предлошка:Math (во математиката и бројни програмски јазициПредлошка:Refn)	математика, физика, хемија, статистика, економија, теорија на информации и инженерство
10	десетичен логаритам	Предлошка:Math	Предлошка:Math, Предлошка:Math (во инженерство, биологија, астрономија)	разни инженерски полиња(види децибел и подолу), логаритамскитаблици, сметала, спектроскопија

Историја

Предлошка:Главна Историјата на логаритмот почнува во седумнаесеттиот век во Европа со откритието на нова функција која прошири сферата на анализата вон опфатот на алгебарските методи. Методот со логаритми првпат бил јавно објавен од Џон Непер во 1614 година во книгата насловена Mirifici Logarithmorum Canonis Descriptio (Опис на чудесното правило на логаритмите). И пред откритието на Непер имало други техники со слични опфати како простаферезата или користењето на таблици на прогресии, кои ги развил Јост Бирги околу 1600 година.

Десетичен логаритам од број е индексот од тој степен на десет кој е еднаков тој број. Кога се зборува за број кој бара толку многу цифри е груба алузија на десетичниот логаритам и истиот Архимед го спомнува како „ред на бројот“. Првите реални логаритми биле евристички методи за множењето да премине во собирање и на тој начин да овозможи брзо пресметување. Некои од овие методи користеле таблици изведени од тригонометриски идентитети. Таквите методи се нарекуваат простафереза.

Откривањето на функцијата денес позната како природен логаритам почнало како обид да се најде површината (квадратура) на правоаголна хипербола на Грегоар де Сен-Венсан, белгиски језуит кој живеел во Прага. Архимед ја напишал Квадратура на парабола во третиот век п.н.е., но квадратурата на хипербола им одолеала на сите напори сè додека Сен-Венсан не ги објавил своите резултати во 1647 година. Односот кој логаритмот го дава меѓу геометриската прогресија и нејзиниот аргумент и аритметичката прогресија од вредности, го поттикнала А. А. де Сараса да ја поврзе квадратурата на Сен-Венсан и логаритмите во простаферезата, што доведува до терминот „хиперболичен логаритам“, синоним за природниот логаритам. Многу брзо новата функција била ценете од Кристијан Хајгенс, Патави и Џемс Грегори. Ознаката log y ја вовел Лајбниц во 1675 година. и следната година го поврзал со интегралот $\int \frac{dy}{y}.$

Логаритамски таблици, логаритмари и историски апликации Предлошка:Anchor

Објаснување на логаритмите во 1797 Енциклопедија британика од 1797 година

Со поедноставувањето на тешките пресметки, логаритмот придонел за напредок на науката, особено на астрономијата. Логаритмот бил од особено значење во геодетските мерења, небесната навигација и други домени. Пјер-Симон Лаплас за логаритмот рекол:

„...волшебен изум кој со намалување на работата од неколку месеци на неколку дена, го удвојува животот на астрономот, го поштедува од грешки и разочарување неодвоиви од долгите пресметки.“

Клучна алатка која овозможила практична примена на логаритмите пред сметалата (дигитроните) и сметачите биле логаритамските таблици. Првата таква таблица била составена од Хенри Бригс (математичар)Хенри Бригс во 1617 година, веднаш по Неперовото откритие. Овие таблици ги содржеле вредностите на Предлошка:Math и Предлошка:Math за кој било број x во одреден опсег, со одредена точност, за одредена основа b (вообичаено Предлошка:Math). На пример, Бригсовата прва таблица ги содржела декадните логаритми од сите цели броеви во опсегот од 1 до 1000 со точност од 14 цифри. Со оглед дека функцијата Предлошка:Math е обратна функција на log_bx, наречена била антилогаритам. Производ и количник на два позитивни броја c и d рутински биле пресметувани како суми и разлика од нивните логаритми. Производот cd или количникот c/d се добива со антилогаритам од сумата или разликата, исто така и од истата табела::

$cd=b^{{\log }_{b}c}{b}^{{\log }_{b}d}=b^{{\log }_{b}c+{\log }_{b}d}$

и

$\frac{c}{d}=c{d}^{-1}=b^{{\log }_{b}c-{\log }_{b}d}.$

За рачни пресметки кои бараат значителна точност, исчитувањето на двата логаритма, пресметувањето на нивната сума или разлика и исчитувањето на антилогаритмот е доста побрз отколку множењето со поранешните методи како простаферезата, која се заснова на тригонометриски идентитети. Пресметката на степени и n-ти корени се сведуваат на множење или делење и исчитувања од таблици:

$c^d={\left(b^{{\log }_{b}c}\right)}^d=b^{d{\log }_{b}c}$

и

$\sqrt[d]{c}=c^{\frac{1}{d}}=b^{\frac{1}{d}{\log }_{b}c}.$

Многу логаритамски таблици ги изразуваат логаритмите како мантиса и одлика од x, односно како целоброен дел и децимален дел од Предлошка:Math. Одликата на Предлошка:Math е еден плус одликата на x, а нивните мантиси се исти. Ова го проширува опфатот на логаритамските таблици: со дадена таблица Предлошка:Math за сите цели броеви x од 1 до 1000, логаритам од 3542 се апроксимира со

${\log }_{10}3542={\log }_{10}(10\cdot 354.2)=1+{\log }_{10}354.2\approx 1+{\log }_{10}354.$ Поголема точност може да се добие со интерполација.

Друга важна апликација бил логаритмарот, пар на логаритамски поделени скали за пресметка како што е илустрирано на сликата.

Шематски приказ на логаритмар. Почнувајќи од 2 на долната скала, се додава растојание од 3 на горната скала и се добива производ 6. Логаритмарот работи бидејќи е обележан така што растојанието од 1 до x е пропорционално на логаритам од x.

Неподвижна логаритамска скала, била измислено кратко по откритието на Непер. Вилијам Отред го подобрил и создал логаритмар – пар на логаритамски скали подвижни една во однос на другата. Броевите се поставени на подвижните скали на растојанија пропорционални на разликите меѓу нивните логаритми. Лизгањето на горната скала соодветствува на механичко додавање логаритми. На пример, со додавање на растојание од 1 до 2 на долната скала на растојанието од 1 до 3 на горната скала дава производ 6, што се отчитува на долниот дел. Логаритмарот бил суштинска алатка за сметање за инженерите и научниците сè до 1970-тите години бидејќи овозможува, за сметка на точноста, многу побрзи пресметки отколку техниките засновани на таблици.

Аналитички својства

За подлабока студија на логаритмите неопходен е концептот на функција (математика)функција. Функција е правило според кое за даден број се добива друг. Пример за функција која го дава Предлошка:Nowrap степен од b од кој било реален број x, каде основата b е фиксен број. Функцијата се запишува: $f(x)=b^x.$

Логаритамска функција

За да се поткрепи дефиницијата за логаритам, неопходно е да се покаже дека равенката

$b^x=y$

има решение x и дека тоа решение е единствено, под услов y да е позитивен, а b е позитивен и различен од 1. За доказ на овој факт потребна е теоремата за средна вредност од елементарната математичка анализа. Според оваа теорема непрекината функција која дава две вредности m и n исто така дава која било вредност која лежи меѓу m и n. Функција е непрекината ако нема "скокови", што значи дека нејзиниот графикон може да се исцрта без подигање на моливот.

Може да се покаже дека ова својство важи за функцијата Предлошка:Math. Бидејќи f може да има произволно големи и произволно мали позитивни вредности, кој било број Предлошка:Math лежи меѓу Предлошка:Math и Предлошка:Math за соодветно Предлошка:Math и Предлошка:Math. Оттука, теоремата за средна вредност осигурува дека равенката Предлошка:Math има решение. Освен тоа, постои само едно решение на оваа равенка, бидејќи функцијата f е монотоно растечка функција (за Предлошка:Math), или монотоно опаѓачка (за Предлошка:Math).

Единственото решение x логаритам од y со основа b, Предлошка:Math. Функцијата која на y му го доделува неговиот логаритам се нарекува логаритамска функција (или само логаритам).

Главната одлика на функцијата Предлошка:Math е формулата за нејзиниот производ

${\log }_b(xy)={\log }_{b}x+{\log }_{b}y.$

поточно, логаритам со која било основа Предлошка:Math е единствената растечка функција f од позитивните реални броеви кои го задоволуваат Предлошка:Math и

$f(xy)=f(x)+f(y).$

Обратна функција

Графиконот на логаритамската функција Предлошка:Math (син) е добиени со рефлектирање на графиконот на функцијата Предлошка:Math (црвен) во однос на дијагоналната линија (Предлошка:Math).

Формулата за логаритам од степен на кој било број x е,

${\log }_b\left(b^x\right)=x{\log }_{b}b=x.$

Искажано со зборови, Предлошка:Math степен на b и потоа логаритам со основа Предлошка:Math дава x. Обратно, за даден позитивен број y, формулата

$b^{{\log }_{b}y}=y$

Кажува дека прво вадење логаритам, а степенување го дава истиот број y. Според тоа, двете можни комбинации од логаритмирање и степенување го даваат оригиналниот број. Значи, логаритам со основа b е обратна функција на Предлошка:Math.

Обраните функции се тесно поврзани со оригиналните функции. Нивните графикони меѓусебно кореспондираат со промена на x и y координатите (или по огледално пресликување на дијагоналната линија x = y), како што е прикажано десно: точката Предлошка:Math на графиконот f одговара на точката Предлошка:Math на графиконот на логаритамот и обратно. Како последица на тоа, log_b(x) дивергираат во бесконечност (станува поголем од кој било даден број) ако x расте во бесконечност, под услов b да е поголем од еден. Во тој случај, Предлошка:Math е растечка функција. За Предлошка:Math, Предлошка:Math тежи кон минус бесконечност. Кога x се приближува до нула, Предлошка:Math оди во минус бесконечност за Предлошка:Math (плус бесконечност за Предлошка:Math, соодветно).

Извод и антиизвод

Графиконот на природниот логаритам (зелен) и неговата тангента во Предлошка:Math (црн)

Аналитичките својства на функциите преминуваат на нивните обратни функции. Така, бидејќи Предлошка:Math е непрекината и диференцијабилна функција, таква е и Предлошка:Math. Приближно, непрекината функција е диференцијабилна ако нејзиниот графикон нема остри „ќошови“. Покрај тоа, како што изводот од Предлошка:Math е Предлошка:Math согласно својствата на експоненцијалната услуга, според правилото за извод од сложени функции изводот од Предлошка:Math е даден си

$\frac{d}{dx}{\log }_{b}x=\frac{1}{x\ln b}.$

Значи, наклонот на тангентата која го допира логаритамот со Предлошка:Math во точката Предлошка:Math е еднаков на Предлошка:Math.

Изводот од ln x е 1/x; ова имплицира дека ln x единствениот антиизвод од Предлошка:Math што има вредност 0 за Предлошка:Math. Ова е многу едноставна формула што навело природниот логаритам да се нарече „природен“; истото е исто така една од главните причини за битноста на константата e.

Изводот со генерализиран функционален аргумент Предлошка:Math е

$\frac{d}{dx}\ln f(x)=\frac{f^{\prime }(x)}{f(x)}.$

Количникот на десната страна се нарекува логаритамски извод од f. Пресметувањето Предлошка:Math со помош на извод од Предлошка:Math е познато како логаритамско диференцирање. Антиизводот од природен логаритам Предлошка:Math е:

$\int \ln (x)dx=x\ln (x)-x+C.$

Соодветните формули, како антиизводи од логаритми со други основи може да се изведат од оваа равенка користејќи промена на основата.

Претставување на природниот логаритам со интеграл

Природен логаритам од t е осенчаната површина под графиконот на функцијата Предлошка:Math (реципрочна на x).

Природен логаритам од t е еднаков на интеграл од 1/x dx од 1 до t:

$\ln (t)=\underset{1}{\overset{t}{\int }}\frac{1}{x}dx.$

Со други зборови, Предлошка:Math е еднаков на површината меѓу оската x и графиконот на функцијата Предлошка:Math, за Предлошка:Math до Предлошка:Math (сликата десно). Ова е последица на основната теорема на анализата и фактот дека извод од Предлошка:Math е Предлошка:Math. Десната страна на оваа равенка може да служи како дефиниција на природен логаритам. Формулите за производ и степен на логаритам може да се изведат од дефиницијата. На пример, формулата за производот Предлошка:Math е изведена како:

$\ln (tu)=\underset{1}{\overset{tu}{\int }}\frac{1}{x}dx\stackrel{(1)}{=}\underset{1}{\overset{t}{\int }}\frac{1}{x}dx+\underset{t}{\overset{tu}{\int }}\frac{1}{x}dx\stackrel{(2)}{=}\ln (t)+\underset{1}{\overset{u}{\int }}\frac{1}{w}dw=\ln (t)+\ln (u).$

Равенството (1) го дели интегралот на два дела, додека равенството (2) е промена на променливата (Предлошка:Math). На долната илустрација, поделбата одговара на површините во жолта и сина боја. Менувајќи ја левата сина страна, вертикално за фактор t и кратејќи ја со истиот фактор хоризонтално не ја менува неговата големина. Поместувајќи ја соодветно, површината повторно одговара на графиконот на функцијата Предлошка:Math. Значи, сината површина на левата страна, која е интеграл од Предлошка:Math од t до tu е иста како интегралот од 1 до u. Ова го поткрепува равенството (2) со погеометриски доказ.

Визуелен доказ за формулата за производ од природен логаритам

Формулата за степен Предлошка:Math може да се изведе на сличен начин:

$\ln (t^r)=\underset{1}{\overset{t^r}{\int }}\frac{1}{x}dx=\underset{1}{\overset{t}{\int }}\frac{1}{w^r}\left(r{w}^{r-1}dw\right)=r\underset{1}{\overset{t}{\int }}\frac{1}{w}dw=r\ln (t).$

Второто равенство користи смена на променливите (интегрирање со смена на променливата), Предлошка:Math.

Збирот од реципрочните вредности од природните броеви,

$1+\frac{1}{2}+\frac{1}{3}+\cdots +\frac{1}{n}=\sum _{k=1}^n\frac{1}{k},$

се нарекува хармониски ред. Тој е тесно поврзан со природниот логаритам: кога n тежнее кон бесконечност, разликата,

$\sum _{k=1}^n\frac{1}{k}-\ln (n),$

конвергира (т.е., доаѓа произволно блиску) кон број познат како Ојлер–Маскерониева константа. Овој врска помага во анализата на перформансите на алгоритми како што е квиксорт.

Постојат и некои други претставувања на логаритмот во форма на интеграл кои се корисни во некои ситуации:

$\ln (x)=-\underset{ϵ\to 0}{\lim }\underset{ϵ}{\overset{\mathrm{\infty }}{\int }}\frac{dt}{t}(e^{-xt}-e^{-t})$

$\ln (x)=\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{dt}{t}[\cos (t)-\cos (xt)]$

Првиот идентитет може да се верифицира со покажување дека тој има иста вредност во Предлошка:Math, и ист извод. Вториот идентитет може да се докаже запишувајќи

$\frac{1}{t}=\underset{0}{\overset{\mathrm{\infty }}{\int }}dq{e}^{-qt}$

и вметнувајќи Лапласова трансформација на Предлошка:Math (и Предлошка:Math).

Трансценденција на логаритмот

Реалните броеви кои не се алгебарски се нарекуваат трансцендентни; на пример, [[Pi|Предлошка:Pi]] и е се такви броеви, но $\sqrt{2-\sqrt{3}}$ не е. Логаритмот е пример за трансцендентна функција. Гелфонд–Шнајдеровата теорема тврди дека вообичаено логаритмите земаат трнсцендентни, т.е., „тешки“ вредности.

Пресметување

Логаритамските копчиња (log за основа 10 и ln за основа e) на типичен научно сметало

Во некои случаи логаритмите лесно се пресметуваат, на пример Предлошка:Math. Во општ случај, логаритмите може да се пресметаат користејќи степенени редови или аритметичко-геометриска средина, или со вадење податоци од претходно пресметанa логаритамска таблица која обезбедува фиксна точност. Њутновиот метод, итеративен метод за приближно решавање на равенки, може исто така да се користи за пресметување логаритам, бидејќи неговата обратна функција, експоненцијалната функција, може ефикасно да се пресмета. Користејќи таблици, за пресметување на логаритми може да се користат методи слични на методата CORDIC, доколку на располагање се само собирањето и поместувањето (шифт) на битови. Освен тоа, двоичниот логаритамски алгоритам го пресметува Предлошка:Math рекурзивно заснован на повторени коренувања на x, искористувајќи ја предноста на релацијата

${\log }_2(x^2)=2{\log }_2(x).$

Степенени редови

Тејлоров ред

Тејлоровиот ред of Предлошка:Math центриран во Предлошка:Math. Анимацијата ги покажува првите  10 апроксимации со 99-тата и 100-тата. Апроксимациите не конвергираат после растојанието од 1 од центарот.

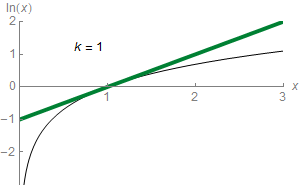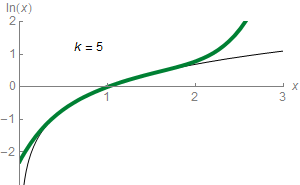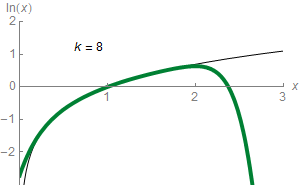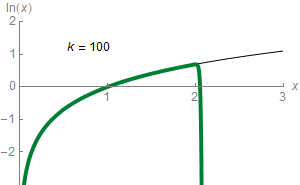
За кој било реален број Предлошка:Mvar кој задоволува Предлошка:Math, важи следната формула:Предлошка:Refn

$\ln (z)=\frac{(z-1{)}^1}{1}-\frac{(z-1{)}^2}{2}+\frac{(z-1{)}^3}{3}-\frac{(z-1{)}^4}{4}+\cdots$

Ова е скратеница за исказот дека Предлошка:Math може да биде апроксимиран до сè поточна вредност со следните изрази:

$\begin{array}{ccc}(z-1)& & \\ (z-1)& -& \frac{(z-1{)}^2}{2}& \\ (z-1)& -& \frac{(z-1{)}^2}{2}& +& \frac{(z-1{)}^3}{3}\\ ⋮& \end{array}$

На пример, со Предлошка:Math третата апроксимација дава 0,4167, што е околу 0,011 повеќе од Предлошка:Math. Овој ред го апроксимира Предлошка:Math со произволна точност, под услов бројот на собироци да е доволно голем. Во елементарната математичка анализа, Предлошка:Math е гранична вредност на редот. Тоа е Тејлоров ред од природен логаритам во Предлошка:Math. Тејлоровиот ред од Предлошка:Math обезбедува особено корисна апроксимација за Предлошка:Math кога Предлошка:Mvar е мал, Предлошка:Math, бидејќи тогаш

$\ln (1+z)=z-\frac{z^2}{2}+\frac{z^3}{3}\cdots \approx z.$

На пример, со Предлошка:Math првата апроксимација дава Предлошка:Math, што е за 5% помала од коректната вредност 0,0953.

Поефикасен ред

Друг ред се заснова на функцијата на површина на хиперболична тангента:

$\ln (z)=2\cdot \mathrm{artanh}\frac{z-1}{z+1}=2(\frac{z-1}{z+1}+\frac{1}{3}{\left(\frac{z-1}{z+1}\right)}^3+\frac{1}{5}{\left(\frac{z-1}{z+1}\right)}^5+\cdots ),$

за кој било реален број Предлошка:Math.Предлошка:Refn Користејќи го сигма обележувањето, истото може да се напише како

$\ln (z)=2\sum _{n=0}^{\mathrm{\infty }}\frac{1}{2n+1}{\left(\frac{z-1}{z+1}\right)}^{2n+1}.$

Овој ред може да се изведе од горниот Тејлоров ред. Истиот конвергира побрзо отколку Тејлоровиот ред особено ако Предлошка:Mvar е блиско до 1. На пример, за Предлошка:Math, првите три члена од вториот ред апроксимира Предлошка:Math со грешка од околу Предлошка:Вред. Брзата конвергенција на Предлошка:Mvar блиско до 1 може да се искористи како предност на следниов начин: за дадена апроксимација со мала точност Предлошка:Math и ставајќи

$A=\frac{z}{\exp (y)},$

логаритмот од Предлошка:Mvar е:

$\ln (z)=y+\ln (A).$

Колку што е првичната апроксимација Предлошка:Mvar е подобра, толку Предлошка:Mvar е поблиска до 1, па неговиот логаритам може да се пресмета ефикасно. Предлошка:Mvar може да се пресмета со користење на експоненцијален ред, кој конвергира брзо под услов Предлошка:Mvar да не е многу голем. Пресметувањето на логаритам од поголем Предлошка:Mvar може да биде сведен на помали вредности за Предлошка:Mvar запишувајќи Предлошка:Math, така што Предлошка:Math.

За пресметување на логаритми од цели броеви може да се искористи тесно поврзан метод. Од горниот ред, следува дека:

$\ln (n+1)=\ln (n)+2\sum _{k=0}^{\mathrm{\infty }}\frac{1}{2k+1}{\left(\frac{1}{2n+1}\right)}^{2k+1}.$

Ако е познат логаритмот на голем цел број Предлошка:Mvar, тогаш редот станува брзо конвергентен ред за Предлошка:Math.

Апроксимација со аритметичко-геометриска средина

Аритметичко-геометриската средина дава апроксимации со голема точност за природен логаритам. Во 1982 година Сасаки и Канада покажале дека истиот бил особено брз за точност меѓу 400 и 1000 децимални места, додека методите со Тејлоров ред биле типично побрзи кога била потребна помала точност. Во нивната работа Предлошка:Math е апроксимиран со точност Предлошка:Math (или p битови на точност) со следната формула (благодарение на Карл Фридрих Гаус):

$\ln (x)\approx \frac{\pi }{2M(1,2^{2-m}/x)}-m\ln (2).$

Тука Предлошка:Math ја означува аритметичко-геометриската средина од x и y. Истата се добива со повторени пресметувања на средната вредност Предлошка:Math (аритметичка средина) и $\sqrt{xy}$ (геометриска средина) од x и y тогаш нека овие два броја станат следните x и y. Двата броја брзо конвергираат кон заедничка гранична вредност чија вредност е Предлошка:Math. m се избира така што

$x{2}^m>2^{p/2}.$

за да се осигура бараната точност. Поголем m прави пресметката на Предлошка:Math да има повеќе чекори (првичните x и y се подалеку, па се потребни повеќе чекори за конвергирање) но дава поголема точност. Константите Предлошка:Math и Предлошка:Math може да се пресметаат со брзоконвергирарчки ред.

Фајнманов алгоритам

Додека работел на проектот Менхетен во Националната лабораторија Лос Аламос, Ричард Фајнман развил алгоритам сличен на алгоритмот за делење кој подоцна бил искористен во Конекшен машин (Connection Machine). Алгоритмот го користи фактот што секој реален број $1<x<2$ е еднозначно претставен како производ од посебни множители во форма $1+2^{-k}$. Алгоритмот секвенцијално го гради тој производ $P$: ако $P\cdot (1+2^{-k})<x$, потоа го менува $P$ во $P\cdot (1+2^{-k})$. Потоа го зголемува $k$ за еден. Алгоритмот запира кога $k$ е доволно голем за да ја даде бараната точност. Бидејќи $\log (x)$ е збир од членови во форма $\log (1+2^{-k})$ што одговараат на оние $k$ за кои множителот $1+2^{-k}$ бил вклучен во производот $P$, $\log (x)$ може да биде пресметан со едноставно собирање користејќи ја таблицата на $\log (1+2^{-k})$ за сите $k$. За логаритамската таблица може да се користи која било основа.

Примена

Наутилус прикажува логаритамска спирала

Логаритмите имаат многу примени во и вон математиката. Некои од овие појави се однесуваат на поимот инваријанса на скалата. На пример, секој простор од школката наутилус е приближна копија од следниот, во размер со константен фактор. Ова води до логаритамска спирала. Бенфордовиот закон за распределба на водечките цифри исто така може да се објасни со инваријанса на скалата. Логаритмите исто така се поврзани со самосличноста. На пример, логаритмите се појавуваат при анализа на алгоритми кои решаваат проблем со негово делење на два помали проблеми и поправајќи ги нивните решенија. Димензиите на самослични геометриски облици, односно облици чии делови личат на целокупната слика се исто така засновани на логаритми. Логаритамските скали се корисни за квантифицирање на релативните промени на вредноста за разлика од нејзината апсолутна разлика. Покрај тоа, бидејќи логаритамската функција Предлошка:Math расте многу бавно за големи x, логаритамските скали се користат за компресија на научни податоци во големи размери (голем однос меѓу малите и големите податоци). Логаритмите исто така постојат во бројни научни формули како во формулата на Циолковски, Фенскеовата равенка, Нернстовата равенка.

Логаритамска скала

Логаритамски графикон кој ја прикажува вредноста на една златна германска марка во хартиени марки за време на германската хиперинфлација во 1920-тите години

Научните количини често се изразуваат како логаритми од други количини користејќи логаритамска скала. На пример, децибелот е единица мерка поврзана со количини на логаритамска скала. Се заснова на десетичниот логаритам од соодносите - 10 пати десетичен логаритам од сооднос на моќности или 20 пати десетичен логаритам од сооднос на напони. Се користи за да се квантифицира загубата на напонски нивоа при пренос на електрични сигнали, да се опишат нивоата на моќност на звуците во акустиката, и апсорпцијата на светлината во полињата на спектрометријата и оптиката. Односот сигнал/шум кој ја опишува количината на несакан шум во однос на сигналот исто така се мери во децибели. На слична тема, вршниот однос сигнал/шум вообичаено се користи за да се оцени квалитетот на звукот и методите на компресија на слика користејќи логаритам.

Силата на земјотресот се мери со земање десетичен логаритам од емитираната енергија. Ова се користи во скалата на моментна магнитуда или во Рихтеровата скала. На пример, земјотрес со магнитуда 5,0 ослободува 32 пати Предлошка:Math, а со магнитуда 6,0 ослободува 1000 пати Предлошка:Math од енергијата на земјотрес со магнитуда 4,0. Друга логаритамска скала е привидната ѕвездена величина. Истата ја мери сјајноста на ѕвездите логаритамски. Уште еден пример е pH во хемијата; pH е минус од десетичниот логаритам од активност од јони од хидрониум (облик на водородни јони Предлошка:Хем во вода). Активноста на хидрониумските јони во неутрална вода е 10⁻⁷ mol•L⁻¹, па оттука pH е 7. Киселината има типичен pH од околу 3. Разликата од 4 соодветствува со односот 10⁴ од активноста, што значи, активноста на хидрониумски јон на киселина е околу Предлошка:Math.

Полулогаритамските графици го користат концептот на логаритамска скала за визуелизација: една оска, вообичаено вертикалната е градирана логаритамски. На пример, графиконот десно го компресира стрмиот пораст од 1 милион на 1 трилиони со истата стапка (на вертикалната оска) како порастот од 1 до 1 милион. На таквите графици, експоненцијалните функции во облик Предлошка:Math се јавуваат како прави линии со наклон еднаков на логаритам од b. Логаритамско-логаритамски графици со двете оски градирани логаритамски, при што функциите во облик Предлошка:Math се изразени како прави линии чиј наклон е еднаков на експонентот k. Ова се применува за визуелизација и анализи на степенени закони.

Психологија

Логаритмите се јавуваат во неколку закони кои ја опишуваат човечката перцепција: Хиковиот закон предлага логаритамски однос меѓу времето кое е потребно да поединци изберат алтернатива и бројот на алтернативи што го имаат. Фитовиот закон предвидува дека потребното време за брзо преместување во целната област е логаритамска функција од растојанието до целта и големината на целта. Во психофизиката, Вебер-Фехнеровиот закон предлага логаритамски однос меѓу дразбата и осетот како што е актуелната спроти перципираната тежина што ја носи едно лице. (Овој „закон“ сепак е понепрецизен од поновите модели како што е Стивенсовиот степенен закон.)

Психолошките студии покажале дека лицата со мало математичко образование тежнеат да ги проценуваат количините логаритамски, односно тие ги позиционираат броевите на необележана линија според нивните логаритми, така што 10 е поставен еднакво блиску до 1000 како што е 100 до 1000. Зголеменото образование го поместува ова кон линеарна процена (позиционирање на 1000 10 пати подалеку) во некои околности, додека логаритмите се користат кога броевите кои треба да се претстават е тешко да се постават линеарно.

Теорија на веројатност и статистика

Три функции за густина на веројатност на случајни променливи со нормални логаритамски распределби. Локацискиот параметар Предлошка:Math, кој е нула за сите три прикажани функции за густина на веројатност, е средна вредност од логаритмот од случајната променлива, не средна вредност од самата променлива.

Распределба на првите цифри (во %, црвени столпчиња) на населението на 237 држави во светот. Црните точки ја означуваат предикцијата на распределба според Бенфордовиот закон.

Логаритмите се јавуваат во теоријата на веројатноста: законот на големите броеви диктира дека, за фер паричка, како што бројот на фрлања на паричката се зголемува кон бесконечност, посматраниот однос на аверси се приближува кон половина. Флуктуациите на овој однос околу една половина се опишани со законот за итеративен логаритам.

Логаритмите исто така се јавуваат и во нормални логаритамски дистрибуции. Кога логаритам од случајна променлива има нормална распределба, се вели дека променливата има нормална логаритамска распределба. Нормалните логаритамски распределби се среќаваат во многу полиња, секаде каде променливата е формирана од производ од бројни независни позитивни случајни променливи, на пример во изучувањето на турбуленција.

Логаритмите се користат за процена на максимална возможност на параметарски статистички модели. За ваков модел, функцијата на возможност зависи од најмалку еден параметар што треба да се процени. Максимумот на функцијата на возможност се јавува при иста параметарска вредност како и максимумот на логаритмот од возможноста ("log возможност"), бидејќи логаритмот е растечка функција. Логаритамската возможност е полесно да се максимизира, особено за мултиплицирани возможности за независни случајни променливи.

Бенфордовиот закон ја опишува појавата на цифри во бројни податочни групи, како што се висини на згради. Според Бенфордовиот закон, веројатноста првата децимална цифра од една ставка во податочниот примерок е d (од 1 до 9) е еднаква Предлошка:Math, без разлика од единицата мерка. Така, може да се очекува дека околу 30% од податоците да имаат прва цифра 1, 18% почнуваат со 2, итн. Ревизорите ги проучуваат девијациите од Бенфордовиот закон за да откријат измамничко сметководство.

Комплексност на пресметки

Анализата на алгоритми е гранка на информатика што ги проучува перформансите на алгоритмите (сметачки програми кои решаваат одреден проблем). Логаритмите се корисни за опишување на алгоритмите кои го делат проблемот на помали делови и се вклучуваат при решавање на потпроблемите.

На пример, да се најде број во подреден список, алгоритам за двоично пребарување го проверува средниот запис и продолжува со половина пред или по средниот запис доколку бројот сè уште не е пронајден. Овој алгоритам во просек бара Предлошка:Math споредби, каде N е должината на списокот. Слично, алгоритмот за сортирање со спојување подредува неподреден список со делење на списокот на половини и подредувајќи ги истите пред да ги спои резултатите. Овој алгоритам типично бара време приближно пропорционално на Предлошка:Math. Тука не е специфицирана основата на логаритмот бидејќи резултатот се менува само за константен фактор кога се користи друга основа. Вообичаено константниот фактор се занемарува при анализата на алгоритми според стандардниот модел на униформен трошок.

За функција Предлошка:Math се вели дека логаритамски расте ако Предлошка:Math е (точно или приближно) пропорционално на логаритам од x. (Биолошките описи на растот на организам, сепак, го користат овој термин за експоненцијална функција.) На пример, кој било природен број N може да биде претставен во двоичниот облик во не повеќе од Предлошка:Math бита. Со други зборови, потребната памтењето за да се складира N расте логаритамски со N.

Ентропија и хаос

Билјард на овална билјардна маса. Две честички, стартувајќи од центарот со агол кој се разликува за еден степен, имаат патеки кои хаотично дивергираат заради рефлексиите на границата.

Ентгропијата е мерка на неред на некој систем. Во статистичката термодинамика, ентропијата S на некој физички систем е дефинирана со

$S=-k\sum _i{p}_i\ln (p_i).$

Сумата е над сите можни состојби i на предметниот систем, како што се позициите на честички гас во контејнер. Освен тоа, Предлошка:Math е веројатност дека состојбата i е достигната и k е Болцмановата константа. Слично, ентропијата во теоријата на информации ја мери количината на информации. Доколку примачот на порака може да очекува која било од N можни пораки со иста веројатност, тогаш количината на информации пренесена со која било таква порака се квантифицира како Предлошка:Math бита.

Љапуновите степени користат логаритми за да го оценат степенот на хаотичност на динамички систем. На пример, за честичка која се движи на овална билјардска маса, дури и мали промени на почетните услови резултираат со многу различни патеки на честичката. Таквите системи се хаотични на детерминистички начин, бидејќи мали грешки во мерењето на почетната состојба предвидливо доведуваат до големи различни конечни состојби. Најмалку еден Љапунов степен на детерминистички хаотичен систем е позитивен.

Фрактали

Шерпињскиев триаголник (десно) е конструиран со повторено заменување на рамностраните триаголници со три помали триаголници.

Логаритмите се јавуваат во дефинициите за димензија на фракталите. Фракталите се геометриски објекти кои се самослични: мали делови ја репродуцираат, барем грубо, целата глобална структура. Шерпињскиевиот триаголник (на сликата) може да се покрие со три негови копии, секоја со страни со половина од должината на оригиналните. Ова ја чини Хаусдорфовата димензија на оваа структура Предлошка:Math. Друго логаритамско засновано обележување е добиено со броење на бројот на кутии потребни за да се покрие предметниот фрактал.

Музика

Логаритмите се поврзани со музичките тонови и интервали. При еднаква темперација, соодносот на честотите зависи само од интервалот меѓу два тона, не од специфичната честота, или висината на звукот, на поединечните тонови. На пример, нотата A има честота од 440 Hz и рамно B има честота од 466 Hz. Интервалот меѓу A и рамно B е полутон, е оној меѓу рамно B и B (честота 493 Hz). Соодветно на тоа, соодносот на честотите е согласно:

$\frac{466}{440}\approx \frac{493}{466}\approx 1.059\approx \sqrt[12]{2}.$

Следствено, логаритмите може да се користат за опис на интервалите: интервалот се мери во полутонови со логаритам Предлошка:Math од соодносот на честоти, додека логаритмот Предлошка:Math од соодносот на честоти го изразува интервалот во центи, стотинки од полутон. Последниот се користи за фино кодирање, како што е потребно за нееднакви темперации.

Интервал (двата тона се свират во исто време)	1/12 тон Предлошка:Audio	Полутон Предлошка:Audio	Природна терца Предлошка:Audio	Терца (интервал) Предлошка:Audio	Тритонус Предлошка:Audio	Октава Предлошка:Audio
Сооднос на честоти r	$2^{\frac{1}{72}}\approx 1,0097$	$2^{\frac{1}{12}}\approx 1,0595$	$\frac{5}{4}=1,25$	$\begin{array}{cc}{2}^{\frac{4}{12}}& =\sqrt[3]{2}\\ & \approx 1,2599\end{array}$	$\begin{array}{cc}{2}^{\frac{6}{12}}& =\sqrt{2}\\ & \approx 1,4142\end{array}$	$2^{\frac{12}{12}}=2$
Соодветниот број на полутонови ${\log }_{\sqrt[12]{2}}(r)=12{\log }_2(r)$	$\frac{1}{6}$	$1$	$\approx 3,8631$	$4$	$6$	$12$
Соодветниот број на центи ${\log }_{\sqrt[1200]{2}}(r)=1200{\log }_2(r)$	$16\frac{2}{3}$	$100$	$\approx 386.31$	$400$	$600$	$1200$

Теорија на броеви

Природните логаритми се тесно поврзани со распределбата на простите броеви (2, 3, 5, 7, 11, ...), битна тема во теоријата на броеви. За кој било цел број x, бројот на прости броеви помали или еднакви на x е изразен со [[функција на распределба на прости броеви|Предлошка:Math]]. Теоремата на прости броеви тврди дека Предлошка:Math е приближно даден со

$\frac{x}{\ln (x)},$

во смисла дека односот Предлошка:Math и дропката се приближува на 1 кога x тежнее кон бесконечност. Следствено, веројатноста дека случајно одбран број меѓу 1 и x е прост е обратнопропорционален на бројот на цифри на x. Далеку подобра процена на Предлошка:Math е дадена со функцијата на интегрален логаритам Предлошка:Math, дефинирана со

$\mathrm{L}\mathrm{i}(x)=\underset{2}{\overset{x}{\int }}\frac{1}{\ln (t)}dt.$

Римановата хипотеза, една од најстарите отворени математички претпоставки, може да се наведе споредувајќи ги Предлошка:Math и Предлошка:Math. Ердеш-Кацовата теорема која го опишува бројот на различни прости делители исто така го вклучува природниот логаритам.

Логаритам од n факториел, Предлошка:Math, е даден со

$\ln (n!)=\ln (1)+\ln (2)+\cdots +\ln (n).$

Ова може да се искористи за да се добие Стирлинговата формула, апроксимација за Предлошка:Math за големи n.

Обопштувања

Комплексен логаритам

Поларен облик на Предлошка:Math. φ и φ' се аргументи од z.

Комплексните броеви a кои е решенија на равенката

$e^a=z.$

се нарекуваат комплексни логаритми. Тука, z е комплексен број. Комплексен број општо се означува како Предлошка:Math, каде x и y се реални броеви, а i е имагинарна единица. Ваков број може визуелно да се претстави со точка во комплексна рамнина, како што е прикажано десно. Поларниот облик кодира ненулов комплексен број z со неговата апсолутна вредност, односно, растојанието r до координатниот почеток, и аголот меѓу x оската и линијата која минува низ координатниот почеток и z. Овој агол се нарекува аргумент на z. Апсолутната вредност r од z е

$r=\sqrt{x^2+y^2}.$

Аргументот не е еднозначно одреден од z: Предлошка:Math и Предлошка:Math' = Предлошка:Math + 2Предлошка:Pi се аргументи на z бидејќи со додавање Предлошка:Math радијани или 360 степениПредлошка:Refn на φ соодветствува на „вртење“ околу координатниот почеток во насока на стрелките на часовникот за круг. Резултатниот комплексен број е повторно z, како што е илустрирано десно. Сепак, точно само еден аргумент Предлошка:Math ги задоволува Предлошка:Math и Предлошка:Math. Истиот се нарекува основен аргумент, се означува Предлошка:Math, со големо A. (Алтернативна нормализација е Предлошка:Math.)

Главната гранка на комплексен логаритам, Log(z). црната точка во Предлошка:Math соодветствува на апсолутна вредност нула, а посветлите бои одговараат на поголеми апсолутни вредности. Тонот на бојата го кодира аргументот на Log(z).

Користејќи ги тригонометриските функции синус и косинус, или комплексен експонент, соодветно, r и φ се такви што следниве идентитети важат:

$\begin{array}{ccc}z& =& r(\cos \phi +i\sin \phi )\\ & =& r{e}^{i\phi }.\end{array}$

Ова значи дека Предлошка:Nowrap степен од e е еднаков на z, каде

$a=\ln (r)+i(\phi +2n\pi ),$

φ е основниот аргумент Arg(z) и n е произволен цел број. Кој било таков a се нарекува комплексен логаритам од z. Постојат бескрајно многу вакви броеви за разлика од еднозначно дефинираните реални логаритми. Ако Предлошка:Math, a се нарекува основна вредност на логаритмот означен Предлошка:Math. Основниот аргумент на кој било позитивен реален број x е 0; оттука Предлошка:Math е реален број и е еднаков на реален (природен) логаритам. Сепак, горните формули за логаритми од производ и степен не ја обопштуваат основната вредност на комплексниот логаритам.

Илустрацијата на десната страна го прикажува Предлошка:Math. Дисконтинуитетот, односно, скокот во тонот во негативниот дел од x, или реалната оска, е предизвикан од скокот на основниот аргумент. Ова место се нарекува одгранување. Ова однесување може да е избегне само со намалување на ограничувањето за φ. Тогаш аргументот на z и, следствено, неговиот логаритам стануваат многузначни функции.

Обратни од други експоненцијални функции

Степенувањето постои во многу области на математиката и нејзината обратна функција често се нарекува логаритам. На пример, логаритмот од матрица е (многузначна) обратна функција од експонент на матрица. Друг пример е p-адичен логаритам, обратна функција на p-адичен експонент. И двата се дефинирани преку Тејлоров ред аналогно со реален случај. Во контекст на диференцијална геометрија, експоненцијалната мапа го мапира тангентниот простор во точката на многукратност во околината на таа точка. Нејзината инверзија се нарекува логаритамска мапа.

Во контекст на конечни групи степенувањето е дадено со повторено множење на еден групен елемент b со самиот себе. Дискретниот логаритам е целобројниот n кој е решение на равенката:

$b^n=x,$

каде x е елемент од групата. Степенувањето може да се изврши ефикасно, но се верува дека е многу тешко да се пресмета дискретниот логаритам во некои групи. Оваа асиметрија има важна примена во криптографија со јавен клуч, како што е на пример случајот со Дифи-Хелмановиот протокол, рутина која обезбедува сигурна размена на криптографски клучеви преку неосигурени информациски канали. Цеховиот логаритам е поврзан со дискретниот логаритам во мултипликативна група од ненулови елементи од конечно поле.

Предлошка:AnchorДруги обратни функции логаритамскослични ги вклучуваат двојниот логаритам ln(ln(x)), супер логаритам (негова мала варијација се нарекува итегриран логаритам во информатиката), Ламбертовата W функција и логит. Тие се обратни функции на двојната експоненцијална функција, тетрација, од Предлошка:Math, и од логистичката функција, соодветно.

Поврзани концепти

Од перспектива на теоријата на групи, идентитетот Предлошка:Math го изразува изоморфизмот на групи меѓу позитивни реални броеви при множење и реалните броеви при собирање. Логаритамските функции се единствените непрекинати изоморфизми меѓу овие групи. Со помош на тој изоморфизам, Харовата мера (Лебегова мера) dx на реалните броеви соодветствува на Харовата мера Предлошка:Math за позитивните реални броеви.

Логаритамските форми Предлошка:Math се јавуваат во комплексната анализа и алгебарската геометрија како диференцијални облици со логаритамски полови.

Полилогаритмот е функција дефинирана со

${\mathrm{Li}}_s(z)=\sum _{k=1}^{\mathrm{\infty }}\frac{z^k}{k^s}.$

Тој е поврзан со природниот логаритам со Предлошка:Math. Покрај тоа, Предлошка:Math е еднаков на Римановата зета функција Предлошка:Math.

Надворешни врски

• Предлошка:Commons category inline
• Khan Academy: Logarithms, free online micro lectures
• Предлошка:Springer
• Предлошка:Citation
• Предлошка:Citation